Question

A person walking 50 metres towards a chimney in a horizontal line, through its base observes that its angle of elevation of its top changes from $30^\circ $ to $45^\circ $. Height of the chimney (in metres) is
A) $25\left( {3 + \sqrt 3 } \right)m$
B) $50\left( {\sqrt 3 + 1} \right)m$
C) $25\left( {\sqrt 3 + 1} \right)m$
D) $25\left( {\sqrt 3 - 1} \right)m$

Answer 1

Hint:In this question we will use trigonometric ratios. Trigonometry is a branch of mathematics which deals with the measurement of sides and angles of a triangle and the problems based on them. Trigonometry helps us to find angles and distances, and is used a lot in science, engineering, and many more.
There are many trigonometry formulas and trigonometric identities, which are used to solve complex equations in geometry.
The ratios of sides of a right-angled triangle with respect to any of its acute angles are known as the trigonometric ratios of that particular angle. They are defined by parameters namely hypotenuse, base and perpendicular.
In ∆ABC
$\tan \theta = \dfrac{{Perpendicular}}{{Base}}$
           

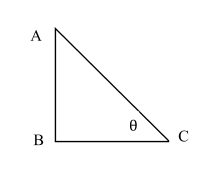
$\tan \theta = \dfrac{{AB}}{{BC}}$
And the value of \[\tan 30^\circ \] is $\dfrac{1}{{\sqrt 3 }}$ and \[\tan 45^\circ \] is 1.

 Complete step by step solution:

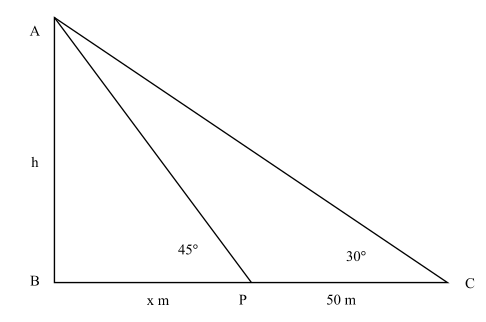
Let the height of chimney be AB = h
It is given that,
The angle of elevation at point C = 30°
A person covers distance towards a chimney till point P = CP = 50 m
Let the distance remaining to reach the chimney = BP = x
As we know that, $\tan \theta = \dfrac{{Perpendicular}}{{Base}}$
$
 \tan 30^\circ = \dfrac{{AB}}{{BC}} \\
 \tan 30^\circ = \dfrac{h}{{x + 50}} \\
 \dfrac{1}{{\sqrt 3 }} = \dfrac{h}{{x + 50}} \\
  h = \dfrac{{x + 50}}{{\sqrt 3 }} \ldots \left( 1 \right) \\
$
Similarly,
$\tan 45^\circ = \dfrac{{AB}}{{BP}}$
$
1 = \dfrac{h}{x} \\
 h = x \ldots \left( 2 \right) \\
$
From equation (1) and (2), we get
$
x = \dfrac{{x + 50}}{{\sqrt 3 }} \\
x = \dfrac{x}{{\sqrt 3 }} + \dfrac{{50}}{{\sqrt 3 }} \\
x - \dfrac{x}{{\sqrt 3 }} = \dfrac{{50}}{{\sqrt 3 }} \\
x\dfrac{{\left( {\sqrt 3 - 1} \right)}}{{\sqrt 3 }} = \dfrac{{50}}{{\sqrt 3 }} \\
x = \dfrac{{\dfrac{{50}}{{\sqrt 3 }}}}{{\dfrac{{\left( {\sqrt 3 - 1} \right)}}{{\sqrt 3 }} \times \left( {\sqrt 3 + 1} \right)}} \times \left( {\sqrt 3 + 1} \right) \\
 x = \dfrac{{50\left( {\sqrt 3 + 1} \right)}}{2} \\
 x = 25\left( {\sqrt 3 + 1} \right)m \\
$

As, x = h
$25\left( {\sqrt 3 + 1} \right)m$
$h = 25\left( {\sqrt 3 + 1} \right)m$

Hence, the correct answer is option ‘c’.

Note: In this kind of problems before solving it we have to draw the diagram and arrange the positions to find the given value of the question.As the problem is based on heights and distance so diagram is important. In this problem, simplification plays a key role to get the correct answer , most of the students will go wrong in this part so focus on simplification is important.