Question

A person of height h standing at the centre of room looking towards a plane mirror hanging on a wall, can see the bottom edge of the wall behind him if minimum length of mirror is:
 A. \[h\]
B. \[{h {\left/ {\vphantom {h 2}} \right. } 2}\]
C. \[h/3\]
D. \[{h {\left/ {\vphantom {h 4}} \right. } 4}\]

Answer 1

Hint: The ray diagram for the given condition is to be drawn along with proper position of plane mirror as well as the position of the wall.
Here in this question we have to apply the concept of similarity of triangles.

Complete step by step answer:
The height of the person is, h
The figure showing the orientation of the mirror is given as,

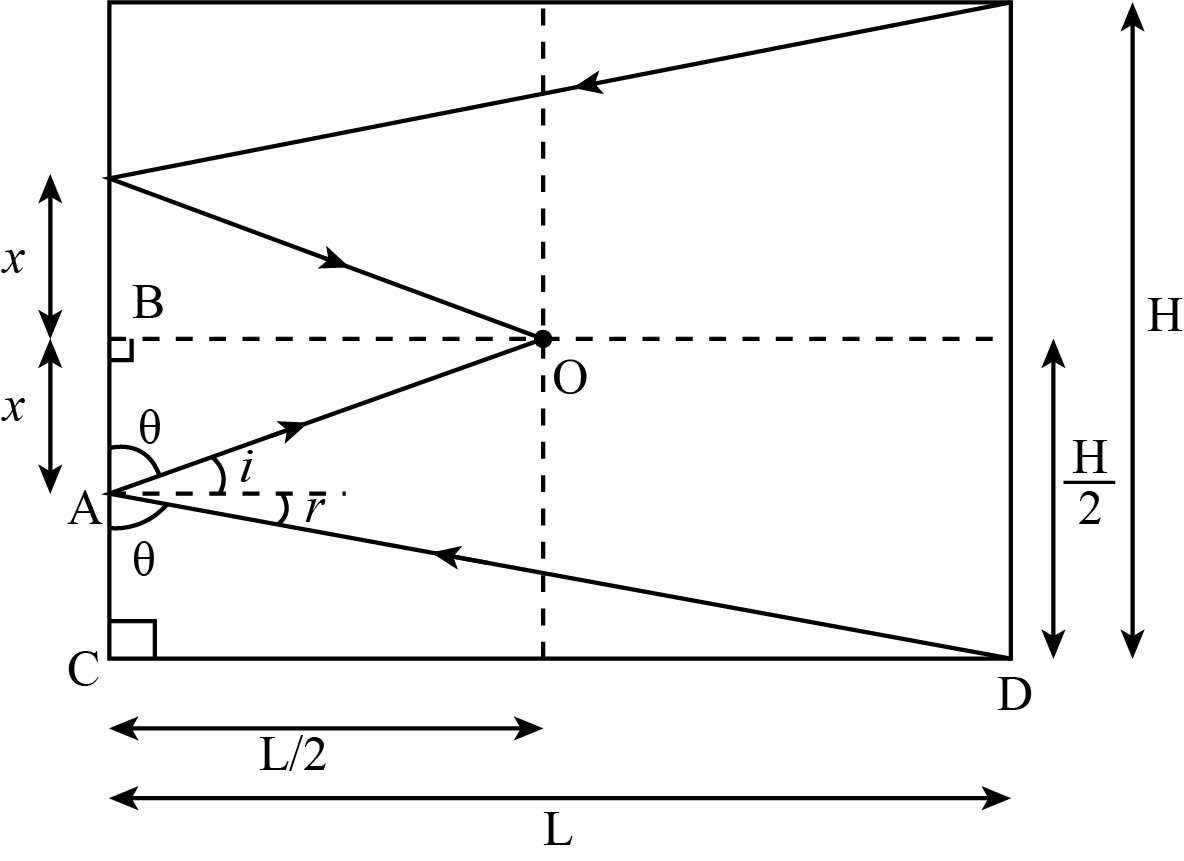
Let the distance between the mirror and the wall be L. Then, from the above figure the length of the mirror is 2x.
Applying the concept of similarity of triangles in the figure. And in triangle OAB and triangle DAC, taking the ratio of similar sides as,
\[\dfrac{{AB}}{{OB}} = \dfrac{{AC}}{{CD}}......................\left( 1 \right)\]
The value for the sides from the figure is given as,
$
AB = x\\
OB = L/2\\
AC = \dfrac{H}{2} - x\\
CD = L
$
Substituting the above values in equation 1 as ,
$
\dfrac{{AB}}{{OB}} = \dfrac{{AC}}{{CD}}\\
\implies \dfrac{x}{{L/2}} = \dfrac{{\dfrac{H}{2} - x}}{L}\\
\implies 3x = \dfrac{H}{2}\\
\implies 2x = \dfrac{H}{3}
$
Therefore, the required length of the mirror is H/3

So, the correct answer is “Option C”.

Note:
The given problem is to be resolved by keeping in mind the proper orientation of the lens or any optical instrument along with the appropriate ray diagrams along the path.
Moreover, to calculate the length of any obstacle, the concept of similarity of figures is to recalled