Question

A particle of mass m is attached to one end of massless spring of force constant k, lying on a frictionless horizontal plane. The other end of the spring is fixed. The particle starts moving from its equilibrium position at time \[t=0\]with an initial velocity \[{{u}_{0}}\].When the speed of the particle is \[0.5{{u}_{0}}\], it collides elastically with a rigid wall. After this collision:
(This question has multiple correct options)
\[\begin{align}
  & \text{A) The speed of the particle when it returns to its equilibrium position is }{{u}_{0}} \\
 & \text{B) The time at which the particle passes through the equilibrium position for the first time is }t=\pi \sqrt{\dfrac{m}{k}} \\
 & \text{C) The time at which the maximum compression occurs is }t=\dfrac{4\pi }{3}\sqrt{\dfrac{m}{k}} \\
 & \text{D) The time at which the particle passes through the equilibrium position for the first time is }t=\dfrac{5\pi }{3}\sqrt{\dfrac{m}{k}} \\
\end{align}\]

Answer 1

Hint: We have given the set-up for a mass which is attached to a massless spring with force constant k and the other end of spring is fixed. And it is given that the mass is collided with the rigid wall and the collision took place is elastic. We have to find which of the given statements are/is right. By using a formula of simple harmonic motion we can verify the statements.
Formula used:
\[\begin{align}
  & v={{v}_{\max }}\cos \omega t \\
 & \omega =\dfrac{2\pi }{T} \\
 & T=2\pi \sqrt{\dfrac{m}{k}} \\
\end{align}\]

Complete answer:
The given set-up can be explained by the given diagram

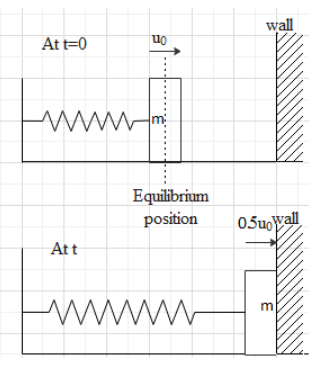
Initially at time \[t=0\]the speed with which the mass m attached to spring is \[{{u}_{0}}\]and it starts to move towards the wall from its equilibrium position. At some time t it collides with the wall and the speed at this instant is \[0.5{{u}_{0}}\].
Now it is given that the collision is elastic collision so mass will rebound with the same speed, i.e. when it reaches back to its equilibrium position its speed will be same when it started the motion which was \[{{u}_{0}}\]. Hence option A is the correct.
Now the next statement is about the time at which the particle will come back to its equilibrium position for the first time. To calculate time, we can use the velocity equation for the particle having simple harmonic motion as after collision the particle will execute simple harmonic motion. The equation of velocity is
\[v={{v}_{\max }}\cos \omega t\]
Where \[{{v}_{\max }}\]is the maximum value of velocity, t is time taken by a particle to reach at which velocity is v and ω is the angular frequency.
Here the maximum velocity is \[{{u}_{0}}\] and so we can substitute value of v as \[0.5{{u}_{0}}\] and t will be the time taken by the particle to reach or hit the wall. So substituting it in the above formula, we get
\[\begin{align}
  & 0.5{{u}_{0}}={{u}_{0}}\cos \omega t \\
 & \Rightarrow \cos \omega t=\dfrac{0.5{{u}_{0}}}{{{u}_{0}}} \\
 & \Rightarrow \omega t={{\cos }^{-1}}\left( 0.5 \right) \\
 & \Rightarrow \omega t=\dfrac{\pi }{3}\text{ }...........\text{(i)} \\
\end{align}\]
Now angular frequency is given as
\[\omega =\dfrac{2\pi }{T}\]
Where T is the time period of one oscillation.
Substituting value of ω in equation (i), we get
\[\begin{align}
  & \left( \dfrac{2\pi }{T} \right)t=\dfrac{\pi }{3} \\
 & \Rightarrow t=\dfrac{\pi T}{6\pi } \\
 & \Rightarrow t=\dfrac{T}{6} \\
\end{align}\]
Now the time period T for simple harmonic motion is given as
\[T=2\pi \sqrt{\dfrac{m}{k}}\]
Hence time t becomes
\[\begin{align}
  & t=\dfrac{2\pi \sqrt{\dfrac{m}{k}}}{6} \\
 & \Rightarrow t=\dfrac{\pi }{3}\sqrt{\dfrac{m}{k}} \\
\end{align}\]
Now the time taken by the particle to reach its equilibrium position for first time will be twice the time taken by it to hit the wall, i.e. 2t, which gives us
\[2t=\dfrac{2\pi }{3}\sqrt{\dfrac{m}{k}}\text{ }............\text{(ii)}\]
Hence option B is wrong.
Now let us find the time at which the particle will come back to its equilibrium position second time. So the particle will first hits the wall and then come back to its initial position and then further continue to moves towards the fixed end of the spring and then again comes back towards the wall hence its initial position which can be shown as

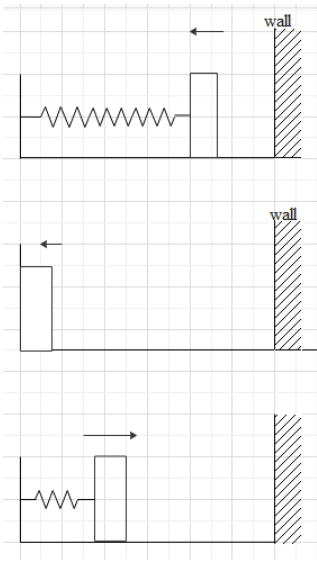
Now suppose the fixed end of the spring is point A and wall B and there is oscillation from A to B and then B to A, then the time period for 1 oscillation is T and so time taken for particle to move from A to B will be \[\dfrac{T}{2}\]. And if the point E that is in equilibrium position lies in between A to B, the time taken by the particle to go from E to B is given as \[\dfrac{T}{6}\] which we calculated above. So the time taken by the particle to move from A to E will be given as \[\dfrac{T}{2}-\dfrac{T}{6}\] which will give us \[\dfrac{T}{4}\]. The diagrammatic representation is

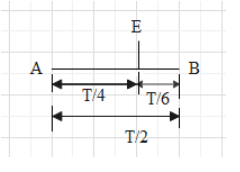
Now the time taken by the particle to pass through equilibrium position will be given as the time taken by it to pass from equilibrium position first time plus the twice the time taken by it to cover the distance from A to E i.e. \[\dfrac{T}{2}\].
If time taken by the particle is t’ then we can write,
\[t'=2t+\dfrac{T}{2}\]
Substituting value of 2t and T from above we have
\[\begin{align}
  & t'=\dfrac{2\pi }{3}\sqrt{\dfrac{m}{k}}+\dfrac{2\pi }{2}\sqrt{\dfrac{m}{k}} \\
 & \Rightarrow t'=\sqrt{\dfrac{m}{k}}\left( \dfrac{2\pi }{3}+\pi \right) \\
 & \Rightarrow t'=\dfrac{5\pi }{3}\sqrt{\dfrac{m}{k}} \\
\end{align}\]
Hence option D is correct.
Now the maximum compression in spring will occur when the particle will hit the fixed end of the spring. And time taken for that will be the time taken to come back to its equilibrium position first time plus the time taken to cover the distance from E to A which is \[\dfrac{T}{4}\] as discussed earlier. If time at which maximum compression occur is t”, then
\[\begin{align}
  & t''=2t+\dfrac{T}{4} \\
 & \Rightarrow t''=\dfrac{2\pi }{3}\sqrt{\dfrac{m}{k}}+\dfrac{2\pi }{4}\sqrt{\dfrac{m}{k}} \\
 & \Rightarrow t''=\sqrt{\dfrac{m}{k}}\left( \dfrac{2\pi }{3}+\dfrac{\pi }{2} \right) \\
 & \Rightarrow t''=\dfrac{7\pi }{6}\sqrt{\dfrac{m}{k}} \\
\end{align}\]
Hence option C is wrong.

Therefore, only option A and D is correct.

Note:
It is multiple correct answer type questions therefore one or more than one option can be right. Also here one complete oscillation will be when the particle moves from E to B, then B to E, then E to A and finally A to E due as it is confusing therefore we consider that one complete oscillation is when the particle covers distance from A to B back and forth.