Question

A particle of mass 200 g is attached to an ideal string of length 1.30 m whose upper end is fixed to the ceiling. The particle is made to revolve in a horizontal circle of radius 50 cm. The tension in the string is \[(g=10{m}/{{{s}^{2}}}\;)\]
\[\begin{align}
  & (1)\,\dfrac{13}{6}N \\
 & (2)\,\dfrac{11}{6}N \\
 & (3)\,\dfrac{26}{5}N \\
 & (4)\,Zero \\
\end{align}\]

Answer 1

Hint: We will be equating the normal force to the vertical component of the string to find the value of the tension in the string, as, the vertical component of the string represents the tension in the string.

Formula used:
\[T=\dfrac{mg}{\cos \theta }\]

Complete step by step solution:
The particle attached to an ideal string with upper end fixed revolving in a horizontal circle forms a cone of radius equal to the radius of the circle and the height being equal to the length of the string.
From the given information, we have the data as follows.
The mass of the particle, \[m=200\,g\]
\[\Rightarrow m=0.2\,kg\]
The length of the string, \[l=1.30\,m\]
The radius of the circle, \[r=50\,m\]
\[r=0.5\,m\]
The acceleration due to gravity, \[g=10\,{m}/{{{s}^{2}}}\;\]
Consider a figure that represents the particle attached to an ideal string with upper end fixed revolving in a horizontal circle.

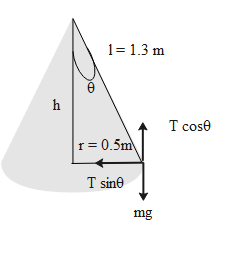
The tension in the string is given by the vertical component. Therefore, the tension in the string is,
\[T\cos \theta =mg\]
Because the vertical component of the tension equals the normal force.
Thus, the tension in the string is,
\[T=\dfrac{mg}{\cos \theta }\]
Now, we will compute the value of the cosine angle.
The cosine angle is given by the formula as follows.
\[\begin{align}
  & \cos \theta =\dfrac{Adj}{Hyp} \\
 & \Rightarrow \cos \theta =\dfrac{h}{l} \\
 & \Rightarrow \cos \theta =\dfrac{\sqrt{{{l}^{2}}-{{r}^{2}}}}{l} \\
\end{align}\]
Substitute the values of length of the string and the radius of the circle in the above formula to find the cosine angle.
\[\begin{align}
  & \cos \theta =\dfrac{\sqrt{{{1.3}^{2}}-{{0.5}^{2}}}}{1.3} \\
 & \therefore \cos \theta =\dfrac{1.2}{1.3} \\
\end{align}\]
As we have obtained the value of the cosine angle, now, we will proceed with the computation of the tension in the string.
Consider the formula for computing the tension in the string.
\[T=\dfrac{mg}{\cos \theta }\]
Substitute the values of the mass of the particle, the acceleration due to gravity and the cosine angle in the above equation.
\[\begin{align}
  & T=\dfrac{0.2\times 10}{{}^{1.2}/{}_{1.3}} \\
 & \Rightarrow T=\dfrac{0.2\times 10\times 1.3}{1.2} \\
 & \Rightarrow T=\dfrac{2.6}{1.2} \\
\end{align}\]
Therefore, the value of the tension in the string is, \[T=\dfrac{13}{6}N\]
\[\therefore \]The value of the tension in the string is \[\dfrac{13}{6}N\], thus, the option (1) is correct.

Note: The units of the parameters should be taken care of. As in this case, the units of the mass of the particle and the radius of the circle weren’t in SI units, so, we changed it to SI units.