Question

A particle moves from a point \[( - 2\hat i + 5\hat j)\;\] to \[(4\hat j + 3\hat k)\] when a force of \[(4\hat i + 3\hat j)\] N is force? How much work has to be done by the force?
A. $8J$
B. $11J$
C. $5J$
D. $2J$

Answer 1

Hint: To solve this question we will take the two points as some two random points then we will find the distance between them by the triangle law then after that finding distance vector, we will find the work by the formula work is equal to the force multiplied by the distance.

Complete answer:
Firstly, we will take A and B some random points in a coordinate system having an origin O. So will prepare one diagram which shows a rough idea about the whole situation which is given in the problem. So, the diagram is as follows,

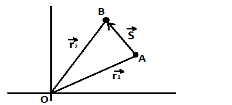
Where point A= \[( - 2\hat i + 5\hat j)\;\] so, ${r_1} = ( - 2\hat i + 5\hat j)\;$
And point B= \[(4\hat j + 3\hat k)\] so, ${r_2} = (4\hat j + 3\hat k)$
Then in the above diagram with the given situation, applying triangle law in the triangle AOB, we get,
${\vec r_1} + \vec S = {\vec r_2}$
$ \Rightarrow \vec S = {\vec r_2} - {\vec r_1}$
$ \Rightarrow \vec S = (4\hat j + 3\hat k) - ( - 2\hat i + 5\hat j)\;$
$ \Rightarrow \vec S = (4\hat j + 3\hat k + 2\hat i - 5\hat j)\;$
$ \Rightarrow \vec S = (2\hat i - \hat j + 3\hat k)\;$
And we have given that the force is,
\[\vec F = (4\hat i + 3\hat j)\]
As we know that the work done is the multiplication of the force vector and the displacement vector.
So, $\vec W = \vec F \times \vec S$
$ \Rightarrow \vec W = (4\hat i + 3\hat j + 0\hat k) \times (2\hat i - \hat j + 3\hat k)\;$
$ \Rightarrow \vec W = (4 \times 2)\hat i - (3 \times 1)\hat j + (0 \times 3)\hat k\;$
$ \Rightarrow \vec W = 8\hat i - 3\hat j$
$ \Rightarrow \left| {\vec W} \right| = 5J$
So, the work done by the force is $5J$.

So, the correct answer is “Option C”.

Note:
Work is the process of energy transfer to the motion of an object via application of a force, often represented as the product of force and displacement. The work may be positive or negative according to the nature of the component of the force which is responsible for the work to be done. A positive work will be done if the force which is being applied has a component in the direction of the displacement of the point of application while the negative work will be done if the force has a component opposite to the direction of the displacement at the point of application of the force.