Question

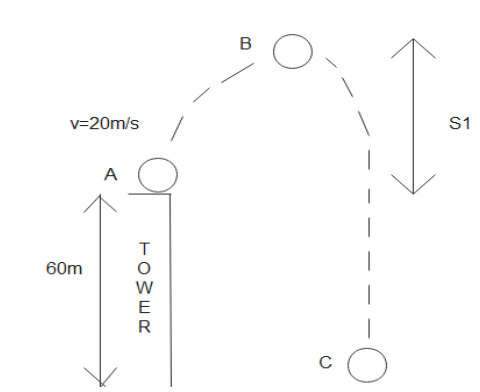
A particle is projected upwards from the roof of a tower 60m high with velocity 20m/s. Find the average speed.

Answer 1

Hint: We have to know that when an object is projected upwards, the only force acting on the object will be the gravitational force. The acceleration due to gravity is a constant and then we have to use the equations of motion which is final velocity is equal to initial velocity plus acceleration into time and then distance is equal to initial velocity into time plus half into acceleration into time squared to determine the average speed of the ball.

Complete Step-By-Step answer:
We have been given that the height of the tower is 60m and the ball travels upwards with velocity 20m/s.

We have known that when we throw an object upwards it reaches to its highest point and only then it will reach the ground.

So, let us take the distance from the tip of the tower to the highest point reached by the ball (from A to B) as \[{{S}_{1}}\] and, let the time taken by the ball to reach the highest point B be taken as \[{{T}_{1}}\].

\[v=u+at\]

This is the formula we will be using to find the value of \[{{T}_{1}}\],
We have,
\[v=0\] (as velocity at the highest point will be zero).
\[u=20m/s\] (given)
\[g=-10m/{{s}^{2}}\] (g is negative as it is against the upward force of the ball).

Now when we substitute the values in the above formula, we get,
$\Rightarrow v=u-g{{T}_{1}} $
$\Rightarrow 0=20-10{{T}_{1}}$
$\Rightarrow -20=-10{{T}_{1}}$
$\Rightarrow {{T}_{1}}=2 sec$
$\Rightarrow s=ut+\dfrac{1}{2}g{{t}^{2}}$ is the formula we will be using to find the value of \[{{S}_{1}}\]

We have,
\[u=20m/s\] (given)
\[g=-10m/{{s}^{2}}\] (g is negative as it against the upward force of the ball)
\[{{T}_{1}}=2\]sec

Now when we substitute the values in the above formula, we get,
\[\begin{align}
  & \Rightarrow {{S}_{1}}=u{{T}_{1}}-\dfrac{1}{2}g{{T}_{1}}^{2} \\
 & \Rightarrow {{S}_{1}}=(20)(2)-\dfrac{1}{2}(10){{(2)}^{2}} \\
 & \Rightarrow {{S}_{1}}=40-20 \\
 & \Rightarrow {{S}_{1}}=20m \\
\end{align}\]

We know that the same time and distance will be covered by the ball to reach the point of projection.

Now when the ball is falling down towards the ground, the velocity of the ball will be 20m/s in the downward direction.

Now, we have to take the time taken for the ball to reach the ground as \[{{T}_{2}}\].
\[s=ut+\dfrac{1}{2}g{{t}^{2}}\] is the formula we will be using to find the value of \[{{T}_{2}}\]
We have,
\[S=60m\] (height from the point of projection to the ground)
\[u=-20m/s\] (acting in downward direction)
\[g=-10m/{{s}^{2}}\]

Now when we substitute the values in the above formula, we get,
\[\begin{align}
  & \Rightarrow -60=-(20){{T}_{2}}-\dfrac{1}{2}(10)T_{2}^{2} \\
 &\Rightarrow -60=-20{{T}_{2}}-5T_{2}^{2} \\
\end{align}\]
$\Rightarrow {{T}_{2}}=2 sec$

Now the total time taken for the ball from the point of projection to the ground will be,
\[\begin{align}
  & \Rightarrow T=2({{T}_{_{1}}})+{{T}_{2}} \\
 & \Rightarrow T=2(2)+2 \\
\end{align}\]
$\Rightarrow T= 6 sec$

Now the total distance from the point of projection to the ground will be,
\[\begin{align}
&\Rightarrow S=2({{S}_{_{1}}})+{{S}_{2}} \\
& \Rightarrow S=2(20)+60 \\
&\Rightarrow S=100m \\
\end{align}\]
\[speed=\dfrac{distance}{time}\] is the formula we will be using to find the average speed of the ball,

Now when we substitute the values in the above formula, we get,
Average speed \[=\dfrac{100}{6}\]\[=16.67m/s\]

Hence, the average speed of the ball is 16.67m/s.

Note:
The projection of any object under the influence of gravity is called projectile motion. We have to be observative when applying signs in the equations used above. The sign for acceleration due to gravity will be negative as it is in the downward direction and acting against the force of the object.