Question

A paper is in the form of a rectangle ABCD where AB = 22cm and BC = 14cm. A semi-circle portion with BC as diameter is cut off. Find the area of the remaining part. $\left( \pi =\dfrac{22}{7} \right)$

Answer 1

Hint: Area of a rectangle can be given by relation length $\times $ breadth and area of circle is given as $\pi {{r}^{2}}$ where r is radius and value of $\pi $ is $\dfrac{22}{7}$. Now, find the remaining area by calculating the difference of the areas of rectangle and semi-circle.

Complete step-by-step answer:
Here, we have a rectangle (paper) ABCD where sides AB = 22cm and BC = 14cm, and we have to determine the area of portion remaining after cutting a semi-circular portion with BC as a diameter. Hence, diagram can be given as

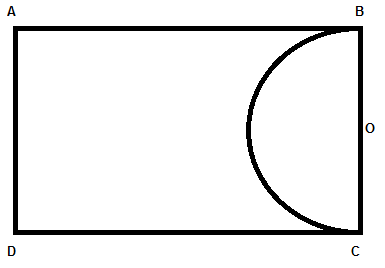
Here O is the center of the semi-circle and mid-point of BC as well.
Hence, radius of semicircle BC is 7cm, i.e., $\left( \dfrac{14}{2} \right)$.
Now, we can get the area of the remaining portion of the rectangle by subtracting the area of the whole rectangle by the area of the semi-circle.
Now, we know
$\begin{align}
& \text{area of rectangle = length }\!\!\times\!\!\text{ breadth} \\
& \text{area of circle = }\pi {{\text{r}}^{2}} \\
\end{align}$
Where r = radius, $\pi =\dfrac{22}{7}$
Hence, area of semicircle $=\dfrac{\pi {{r}^{2}}}{2}$
So, we can get area of remaining part from the given diagram as
Remaining area = $AB\times BC-\dfrac{\pi {{r}^{2}}}{2}$
$=22\times 14-\dfrac{22}{7}\times \dfrac{1}{2}\times {{\left( 7 \right)}^{2}}$
$\begin{align}
 & =308-11\times 7 \\
 & =308-77 \\
 & =231c{{m}^{2}} \\
\end{align}$
Hence, the area of the remaining part can be given as 231 sq. cm.
So, option (B) is the correct answer.

Note:
One may get confused between the formula of area and circumference of a circle. So, one may go wrong while using the area of the circle as $2\pi r$. Hence, be clear with the formula of areas of standard shapes.
One may get confused with the center of the semicircle that is the midpoint of BC. It’s because BC is the diameter of a semi-circle and the midpoint of diameter is center.