
A number consists of 7 digits whose sum is 59. Prove that the chances of it being divisible by 11 is $\dfrac{4}{21}$.
Answer
604.2k+ views
Hint: Divisibility rule of 11 for any number can be given as “any number will be divisible by ‘11’ if the difference of sum of digits at odd places and sum of digits at even places is multiple of 11. Find the total number of cases for numbers with sum 59 and divisible by 11 to get probability.
Complete step by step solution:
We know that any given number will be divisible by 11 if the difference of sum of digits at odd places and sum of digits at even places is multiple of 11.
Hence, there will be 4 digits at odd places and 3 digits at even places in a seven digit number.
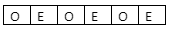
Here ‘O’ represents odd places and ‘E’ represents even places.
So, the sum of digits of a given number is 59.
Let us suppose the sum of digits at odd places be ‘x’ and the sum of digits at even places be ‘y’.
Hence, we can write an equation in terms of x and y as
x + y =59 ……………………… (i)
As we know maximum sum possible for any 7 digit number would be $9\times 7=63\left( 9999999 \right).$
Hence, seven digit numbers for the sum 59 can be given by using following digits:
(i) 9,9,9,9,9,9,5
(ii) 9,9,9,9,9,8,6
(iii) 9,9,9,9,9,7,7
(iv) 9,9,9,9,8,8,7
(v) 9,9,9,8,8,8,8
Now, we can get a total of possible seven digit numbers of sum 59 by permuting / arranging the above given cases.
So, we know that we can arrange ‘n’ things of which ${{r}_{1}}$ of one type, ${{r}_{2}}$of another type, ${{r}_{3}}$ of another, and similarly ${{r}_{p}}$ is of another is give as $\dfrac{n!}{{{r}_{1}}!{{r}_{2}}!{{r}_{3}}!.......{{r}_{p}}!}.$
So, total number of permutations can be given as
$\begin{align}
& \left( i \right)\dfrac{7!}{6!}=7 \\
& \left( ii \right)\dfrac{7!}{5!}=7\times 6=42 \\
& \left( iii \right)\dfrac{7!}{5!2!}=21 \\
& \left( iv \right)\dfrac{7!}{4!2!}=105 \\
& \left( v \right)\dfrac{7!}{3!4!}=\dfrac{7\times 6\times 5}{6}=35 \\
\end{align}$
Hence, total possible numbers of sum of digits 59 is given as = 7+42+21+105+35 = 210
So, the total number of sample spaces is 210.
Now, we can form another equation in ‘x’ and ‘y’ by using the property of divisibility rule of 11 such that
x – y = 11k ……………… (ii)
Where k = 0,1,2…..
Now, we can solve equation (i) and (ii) to get ‘x’ and ‘y’.
So, adding equation (i) and (ii), we get
2x = 11k + 59
$x=\dfrac{11k+59}{2}$ ………………… (iii)
And subtracting both equations (i) and (ii), we get
2y =59 – 11k
$y=\dfrac{59-11k}{2}$ ………………… (iv)
Now, we can observe that k should be an odd number starting from ‘1’. As if we put the value of ‘k’ as an even number, and the sum or difference of even and odd (i.e., 59) will always be odd and then the values of ‘x’ and ‘y’ will be in fraction. And the sum of digits of any number can not be a fraction. Hence, put k = 1 in equation (iii) and (iv), we get
x = 35, y = 24.
Now, for formation of total sum of 24(sum of digits at even place) with three numbers, following combinations are possible for it:
(i) 8,8,8
(ii) 7,8,9
(iii) 6,9,9
Now, permutations of cases can be given as
$\begin{align}
& \left( i \right)\dfrac{3!}{3!}=1 \\
& \left( ii \right)3!=6 \\
& \left( iii \right)\dfrac{3!}{2!}=3 \\
\end{align}$
Hence, for sum 24, total ways = 10
For formation of total sum of 35 with four numbers, the following conditions are possible:
(i) 9998
Hence, total permutations of above case $=\dfrac{4!}{3!}=4.$
Therefore, total number of arrangements of seven digits with sum at even place be 24 and sum ‘35’ at odd place be
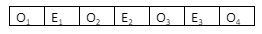
Number of permutations of ${{O}_{1}}{{O}_{2}}{{O}_{3}}{{O}_{4}}=4$
Number of permutations of ${{E}_{1}}{{E}_{2}}{{E}_{3}}=10$
Hence, total numbers of 7 digits with sum 59 and divisible by 11 can be given as $=4\times 10=40$
Now, we can put k = 3 to values of ‘x’ and ‘y’ in equation (iii) and (iv), so we get
x = 46 and y = 13
But the sum of four numbers can never be 46.
Hence, k can never take value except ‘1’ as the sum of four digits will become higher and higher.
So, total number of seven digits with sum 59 which will be divisible by 11 = 40
Total numbers possible of 7 digits with sum 59 = 210
Probability that number is divisible by 11 is
$=\dfrac{40}{210}=\dfrac{4}{21}$
Hence, the given statement is proved.
Note: Don’t miss any cases in these kinds of questions of permutations and combinations. Answers will be wrong by missing one number also, so be careful and check twice of all possibilities of cases for sums of digits of 59, 35 and 24.
Total number of permutations of 7 digits numbers with divisibility 11 is given by = number of arrangement of even places $\times $ number of arrangement of odd places
One can take the value of ‘k’ as only ‘1’ because there is no possible value of k except ‘1’, we can verify it as well. So be careful with that part of the solution as well.
Complete step by step solution:
We know that any given number will be divisible by 11 if the difference of sum of digits at odd places and sum of digits at even places is multiple of 11.
Hence, there will be 4 digits at odd places and 3 digits at even places in a seven digit number.
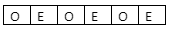
Here ‘O’ represents odd places and ‘E’ represents even places.
So, the sum of digits of a given number is 59.
Let us suppose the sum of digits at odd places be ‘x’ and the sum of digits at even places be ‘y’.
Hence, we can write an equation in terms of x and y as
x + y =59 ……………………… (i)
As we know maximum sum possible for any 7 digit number would be $9\times 7=63\left( 9999999 \right).$
Hence, seven digit numbers for the sum 59 can be given by using following digits:
(i) 9,9,9,9,9,9,5
(ii) 9,9,9,9,9,8,6
(iii) 9,9,9,9,9,7,7
(iv) 9,9,9,9,8,8,7
(v) 9,9,9,8,8,8,8
Now, we can get a total of possible seven digit numbers of sum 59 by permuting / arranging the above given cases.
So, we know that we can arrange ‘n’ things of which ${{r}_{1}}$ of one type, ${{r}_{2}}$of another type, ${{r}_{3}}$ of another, and similarly ${{r}_{p}}$ is of another is give as $\dfrac{n!}{{{r}_{1}}!{{r}_{2}}!{{r}_{3}}!.......{{r}_{p}}!}.$
So, total number of permutations can be given as
$\begin{align}
& \left( i \right)\dfrac{7!}{6!}=7 \\
& \left( ii \right)\dfrac{7!}{5!}=7\times 6=42 \\
& \left( iii \right)\dfrac{7!}{5!2!}=21 \\
& \left( iv \right)\dfrac{7!}{4!2!}=105 \\
& \left( v \right)\dfrac{7!}{3!4!}=\dfrac{7\times 6\times 5}{6}=35 \\
\end{align}$
Hence, total possible numbers of sum of digits 59 is given as = 7+42+21+105+35 = 210
So, the total number of sample spaces is 210.
Now, we can form another equation in ‘x’ and ‘y’ by using the property of divisibility rule of 11 such that
x – y = 11k ……………… (ii)
Where k = 0,1,2…..
Now, we can solve equation (i) and (ii) to get ‘x’ and ‘y’.
So, adding equation (i) and (ii), we get
2x = 11k + 59
$x=\dfrac{11k+59}{2}$ ………………… (iii)
And subtracting both equations (i) and (ii), we get
2y =59 – 11k
$y=\dfrac{59-11k}{2}$ ………………… (iv)
Now, we can observe that k should be an odd number starting from ‘1’. As if we put the value of ‘k’ as an even number, and the sum or difference of even and odd (i.e., 59) will always be odd and then the values of ‘x’ and ‘y’ will be in fraction. And the sum of digits of any number can not be a fraction. Hence, put k = 1 in equation (iii) and (iv), we get
x = 35, y = 24.
Now, for formation of total sum of 24(sum of digits at even place) with three numbers, following combinations are possible for it:
(i) 8,8,8
(ii) 7,8,9
(iii) 6,9,9
Now, permutations of cases can be given as
$\begin{align}
& \left( i \right)\dfrac{3!}{3!}=1 \\
& \left( ii \right)3!=6 \\
& \left( iii \right)\dfrac{3!}{2!}=3 \\
\end{align}$
Hence, for sum 24, total ways = 10
For formation of total sum of 35 with four numbers, the following conditions are possible:
(i) 9998
Hence, total permutations of above case $=\dfrac{4!}{3!}=4.$
Therefore, total number of arrangements of seven digits with sum at even place be 24 and sum ‘35’ at odd place be
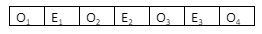
Number of permutations of ${{O}_{1}}{{O}_{2}}{{O}_{3}}{{O}_{4}}=4$
Number of permutations of ${{E}_{1}}{{E}_{2}}{{E}_{3}}=10$
Hence, total numbers of 7 digits with sum 59 and divisible by 11 can be given as $=4\times 10=40$
Now, we can put k = 3 to values of ‘x’ and ‘y’ in equation (iii) and (iv), so we get
x = 46 and y = 13
But the sum of four numbers can never be 46.
Hence, k can never take value except ‘1’ as the sum of four digits will become higher and higher.
So, total number of seven digits with sum 59 which will be divisible by 11 = 40
Total numbers possible of 7 digits with sum 59 = 210
Probability that number is divisible by 11 is
$=\dfrac{40}{210}=\dfrac{4}{21}$
Hence, the given statement is proved.
Note: Don’t miss any cases in these kinds of questions of permutations and combinations. Answers will be wrong by missing one number also, so be careful and check twice of all possibilities of cases for sums of digits of 59, 35 and 24.
Total number of permutations of 7 digits numbers with divisibility 11 is given by = number of arrangement of even places $\times $ number of arrangement of odd places
One can take the value of ‘k’ as only ‘1’ because there is no possible value of k except ‘1’, we can verify it as well. So be careful with that part of the solution as well.
Recently Updated Pages
Master Class 8 Maths: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 7 Maths: Engaging Questions & Answers for Success

Class 7 Question and Answer - Your Ultimate Solutions Guide

Master Class 6 Maths: Engaging Questions & Answers for Success

Class 6 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

Which animal has three hearts class 11 biology CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




