Question

(a) Name two factors on which the magnitude of an induced emf in secondary coil depends.
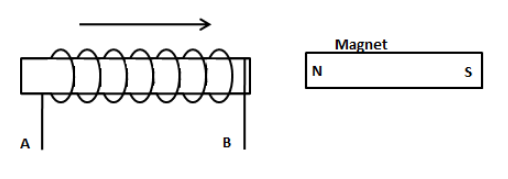
(b) In the diagram below the arrow shows the direction of motion of the coil towards a bar magnet.
(i) State in which direction the current flows, A to B or B to A?
(ii) Name the law used to come to the conclusion.

Answer 1

Hint: Faraday’s law of electromagnetic induction states that the changing magnetic flux induces the emf in the coil. Recall Lenz’s law to determine the direction of the induced current in the coil. According to Lenz’s law; the direction of the induced current in the coil is such that the magnetic field induced by this current opposes the change in the magnetic field which created it in the first place.

Complete step by step answer:
(a) We have from Faraday’s law of electromagnetic induction; the changing magnetic flux induces the emf in the coil. The magnitude of the induced emf in the coil is given by the expression,
\[e = N\dfrac{{d\phi }}{{dt}}\]
Here, N is the number of turns of the coil and \[\phi \] is the magnetic flux due to the magnetic field.
From the above expression, we can infer that, the emf induced in the secondary coil depends on,
-The number of turns of the secondary coil.
-The rate of change of magnetic flux around the secondary coil.

(b) (i) We know that the direction of the induced emf in the coil is given by Lenz’s law. According to Lenz’s law; the direction of the induced current in the coil is such that the magnetic field induced by this current opposes the change in the magnetic field which created it in the first place.

Since the coil is brought closer to the north pole of the magnet, the magnetic field will be induced in the coil such that it can oppose the magnetic field of the bar magnet. Therefore, we can observe, the North Pole will be formed near the right end of the coil. We know that the direction of the magnetic field lines is from the North Pole to the South Pole.

Now, using the right-hand thumb rule, we can determine the direction of the induced current in the coil. According to the right-hand thumb rule, if we hold the current carrying conductor in our right hand such that the curled fingers around the conductor denotes the direction of the magnetic field; then the thumb represents the direction of the current. Therefore, we can see, the direction of the current in the coil is anticlockwise. That is from B to A.

(b) (ii) We have determined the direction of the current in the coil using Lenz’s law as discussed in the above text.

Note:The Faraday’s law of electromagnetic induction cannot tell the direction of the induced current in the loop. The negative sign for the induced sign implies that the induced emf opposes the change in the magnetic flux. For the coil with a single turn, you can express the induced emf as \[e = \dfrac{{d\phi }}{{dt}}\]. The magnetic flux also depends on the current in the coil and permeability of the medium.