A metallic right circular cone 20 cm high and whose vertical angle \[60^\circ \] is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained is drawn into a wire of diameter \[\dfrac{1}{{16}}\] cm, find the length of the wire.
Answer
Verified485.4k+ views
Hint: Here, we need to find the length of the wire. First, we will use the semi-vertical angle formed by the height at the vertex, and trigonometric ratio of tangent to find the radii of the bases of the frustum. Then, we will use the formula for volume of frustum to find the volume. We will use the formula for volume of cylinder to find the volume of the cylindrical wire. Finally, we will use the given information to form an equation and solve it to find the length of the wire.
Formula used:
We will use the following formulas:
1.The tangent of an angle \[\theta \] in a right angled triangle is given by \[\tan \theta = \dfrac{{{\rm{Perpendicular}}}}{{{\rm{Base}}}}\].
2.The volume of the frustum of a cone is given by the formula \[\dfrac{1}{3}\pi h\left( {{R^2} + {r^2} + Rr} \right)\], where \[r\] is the radius of the smaller base of the frustum, \[R\] is the radius of the larger base of the frustum, and \[h\] is the height of the frustum.
3.The volume of the cylinder is given by the formula \[\pi {r^2}h\], where \[r\] is the radius of the base and \[h\] is the height of the cylinder.
Complete step-by-step answer:
First, we will draw the figure using the given information.
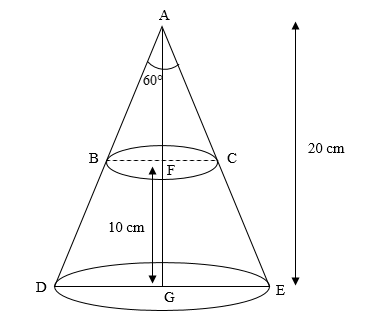
Here, angle DAE is the vertical angle of the cone measuring \[60^\circ \]. AG is the height of the cone, that is 20 cm. GE is the radius of the base of the cone.
FC is the radius of the smaller base of the frustum, and GE is the radius of the larger base of the frustum.
It is given that the cone is cut by a plane parallel to its base at the middle of the height.
Thus, F is the mid-point of AG.
Therefore, we get
\[AF = FG = \dfrac{1}{2}AG\]
Substituting \[AG = 20\] cm in the equation, we get
\[\begin{array}{l} \Rightarrow AF = FG = \dfrac{1}{2} \times 20\\ \Rightarrow AF = FG = 10\end{array}\]
Thus, we get the height FG of the frustum as 10 cm.
Now, the vertical angle DAE is cut into two equal angles by the height.
Therefore, using the figure, we get
\[ \Rightarrow \angle DAG = \angle GAE = \dfrac{1}{2}\angle DAE\]
Substituting \[\angle DAE = 60^\circ \] in the equation, we get
\[\begin{array}{l} \Rightarrow \angle DAG = \angle GAE = \dfrac{1}{2} \times 60^\circ \\ \Rightarrow \angle DAG = \angle GAE = 30^\circ \end{array}\]
Since \[\angle GAE = 30^\circ \], we get \[\angle FAC = 30^\circ \].
Next, we will find the radii of the smaller base and larger base of the frustum.
We know that the tangent of an angle \[\theta \] in a right angled triangle is given by \[\tan \theta = \dfrac{{{\rm{Perpendicular}}}}{{{\rm{Base}}}}\].
Therefore, in triangle AFC, we have
\[ \Rightarrow \tan \angle FAC = \dfrac{{FC}}{{AF}}\]
Substituting \[\angle FAC = 30^\circ \] and \[AF = 10\] cm in the equation, we get
\[ \Rightarrow \tan 30^\circ = \dfrac{{FC}}{{10}}\]
The tangent of the angle measuring \[30^\circ \] is equal to \[\dfrac{1}{{\sqrt 3 }}\].
Substituting \[\tan 30^\circ = \dfrac{1}{{\sqrt 3 }}\] in the expression, we get
\[ \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{{FC}}{{10}}\]
Multiplying both sides of the equation by 10, we get
\[ \Rightarrow FC = \dfrac{{10}}{{\sqrt 3 }}\]
Rationalising the denominator by multiplying and dividing the expression by \[\sqrt 3 \], we get
\[\begin{array}{l} \Rightarrow FC = \dfrac{{10}}{{\sqrt 3 }} \times \dfrac{{\sqrt 3 }}{{\sqrt 3 }}\\ \Rightarrow FC = \dfrac{{10\sqrt 3 }}{3}\end{array}\]
Thus, we get the radius of the smaller base of the frustum as \[\dfrac{{10\sqrt 3 }}{3}\] cm.
Using the formula for tangent in triangle AGE, we have
\[ \Rightarrow \tan \angle GAE = \dfrac{{GE}}{{AG}}\]
Substituting \[\angle GAE = 30^\circ \] and \[AG = 20\] cm in the equation, we get
\[ \Rightarrow \tan 30^\circ = \dfrac{{GE}}{{20}}\]
Substituting \[\tan 30^\circ = \dfrac{1}{{\sqrt 3 }}\] in the expression, we get
\[ \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{{GE}}{{20}}\]
Multiplying both sides of the equation by 20, we get
\[ \Rightarrow GE = \dfrac{{20}}{{\sqrt 3 }}\]
Rationalising the denominator by multiplying and dividing the expression by \[\sqrt 3 \], we get
\[\begin{array}{l} \Rightarrow GE = \dfrac{{20}}{{\sqrt 3 }} \times \dfrac{{\sqrt 3 }}{{\sqrt 3 }}\\ \Rightarrow GE = \dfrac{{20\sqrt 3 }}{3}\end{array}\]
Thus, we get the radius of the larger base of the frustum as \[\dfrac{{20\sqrt 3 }}{3}\] cm.
Now, we will calculate the volume of the frustum of the cone formed.
Substituting \[h = 10\] cm, \[R = \dfrac{{20\sqrt 3 }}{3}\] cm, and \[r = \dfrac{{10\sqrt 3 }}{3}\] cm in the formula for volume of the frustum,\[\dfrac{1}{3}\pi h\left( {{R^2} + {r^2} + Rr} \right)\], we get
Volume of frustum \[ = \dfrac{1}{3}\pi \times 10\left[ {{{\left( {\dfrac{{20\sqrt 3 }}{3}} \right)}^2} + {{\left( {\dfrac{{10\sqrt 3 }}{3}} \right)}^2} + \left( {\dfrac{{20\sqrt 3 }}{3}} \right)\left( {\dfrac{{10\sqrt 3 }}{3}} \right)} \right]\]
Applying the exponents on the bases, we get
\[ \Rightarrow \] Volume of frustum \[ = \dfrac{1}{3}\pi \times 10\left[ {\dfrac{{400 \times 3}}{9} + \dfrac{{100 \times 3}}{9} + \left( {\dfrac{{20\sqrt 3 }}{3}} \right)\left( {\dfrac{{10\sqrt 3 }}{3}} \right)} \right]\]
Multiplying the terms in the expression, we get
\[ \Rightarrow \] Volume of frustum \[ = \dfrac{{10}}{3}\pi \left[ {\dfrac{{400}}{3} + \dfrac{{100}}{3} + \dfrac{{200}}{3}} \right]\]
Adding the terms in the bracket, we get
\[ \Rightarrow \] Volume of frustum \[ = \dfrac{{10}}{3}\pi \left[ {\dfrac{{700}}{3}} \right]\]
Multiplying the terms in the expression, we get
\[ \Rightarrow \] Volume of frustum \[ = \dfrac{{7000}}{9}\pi \]
Now, we will calculate the volume of the cylindrical wire.
The radius of the cylinder wire is half of its diameter, that is \[r = \dfrac{d}{2}\].
Substituting \[d = \dfrac{1}{{16}}\] cm in the expression, we get
\[ \Rightarrow r = \dfrac{{\dfrac{1}{{16}}}}{2}\]
Simplifying the expression, we get
\[ \Rightarrow r = \dfrac{1}{{32}}\] cm
Let the length of the cylindrical wire be \[x\] cm.
Substituting \[h = x\] cm and \[r = \dfrac{1}{{32}}\] cm in the formula for volume of the cylindrical wire, \[\pi {r^2}h\], we get
Volume of cylindrical wire \[ = \pi \times {\left( {\dfrac{1}{{32}}} \right)^2} \times x\]
Multiplying the terms in the expression, we get
\[ \Rightarrow \] Volume of cylindrical wire \[ = \dfrac{{\pi x}}{{1024}}\]
Now, it is given that the wire is drawn out from the frustum.
This means that the metal used to make the frustum is drawn into the cylindrical wire.
Therefore, the volume of the frustum is equal to the volume of the cylindrical wire.
Therefore, we get the equation
\[ \Rightarrow \dfrac{{7000}}{9}\pi = \dfrac{{\pi x}}{{1024}}\]
This is a linear equation in terms of \[x\]. We will solve this to find the value of \[x\], and hence, the length of the cylindrical wire.
Simplifying the equation, we get
\[ \Rightarrow \dfrac{{7000}}{9} = \dfrac{x}{{1024}}\]
Multiplying both sides of the equation by 1024, we get
\[ \Rightarrow \dfrac{{7000}}{9} \times 1024 = x\]
Simplifying the expression, we get
\[ \Rightarrow x = \dfrac{{7168000}}{9}\] cm
Rewriting the expression in decimals and rounding the value, we get
\[\begin{array}{l} \Rightarrow x = 796444.44\\ \Rightarrow x \approx 796444\end{array}\]
Therefore, the value of \[x\] is 796444 cm.
This can be written as \[7964.44\] metres.
Thus, the length of the wire is approximately \[7964.44\] metres.
Note: We have not substituted \[\pi = \dfrac{{22}}{7}\] because they can get cancelled out in the equation \[\dfrac{{7000}}{9}\pi = \dfrac{{\pi x}}{{1024}}\]. Therefore, substituting the value and multiplying them earlier is not required.
We can make a mistake by using the given value \[\dfrac{1}{{16}}\] cm as radius. It is the diameter, and not radius. So, we need to divide the diameter by 2 to get the radius.
Formula used:
We will use the following formulas:
1.The tangent of an angle \[\theta \] in a right angled triangle is given by \[\tan \theta = \dfrac{{{\rm{Perpendicular}}}}{{{\rm{Base}}}}\].
2.The volume of the frustum of a cone is given by the formula \[\dfrac{1}{3}\pi h\left( {{R^2} + {r^2} + Rr} \right)\], where \[r\] is the radius of the smaller base of the frustum, \[R\] is the radius of the larger base of the frustum, and \[h\] is the height of the frustum.
3.The volume of the cylinder is given by the formula \[\pi {r^2}h\], where \[r\] is the radius of the base and \[h\] is the height of the cylinder.
Complete step-by-step answer:
First, we will draw the figure using the given information.
Here, angle DAE is the vertical angle of the cone measuring \[60^\circ \]. AG is the height of the cone, that is 20 cm. GE is the radius of the base of the cone.
FC is the radius of the smaller base of the frustum, and GE is the radius of the larger base of the frustum.
It is given that the cone is cut by a plane parallel to its base at the middle of the height.
Thus, F is the mid-point of AG.
Therefore, we get
\[AF = FG = \dfrac{1}{2}AG\]
Substituting \[AG = 20\] cm in the equation, we get
\[\begin{array}{l} \Rightarrow AF = FG = \dfrac{1}{2} \times 20\\ \Rightarrow AF = FG = 10\end{array}\]
Thus, we get the height FG of the frustum as 10 cm.
Now, the vertical angle DAE is cut into two equal angles by the height.
Therefore, using the figure, we get
\[ \Rightarrow \angle DAG = \angle GAE = \dfrac{1}{2}\angle DAE\]
Substituting \[\angle DAE = 60^\circ \] in the equation, we get
\[\begin{array}{l} \Rightarrow \angle DAG = \angle GAE = \dfrac{1}{2} \times 60^\circ \\ \Rightarrow \angle DAG = \angle GAE = 30^\circ \end{array}\]
Since \[\angle GAE = 30^\circ \], we get \[\angle FAC = 30^\circ \].
Next, we will find the radii of the smaller base and larger base of the frustum.
We know that the tangent of an angle \[\theta \] in a right angled triangle is given by \[\tan \theta = \dfrac{{{\rm{Perpendicular}}}}{{{\rm{Base}}}}\].
Therefore, in triangle AFC, we have
\[ \Rightarrow \tan \angle FAC = \dfrac{{FC}}{{AF}}\]
Substituting \[\angle FAC = 30^\circ \] and \[AF = 10\] cm in the equation, we get
\[ \Rightarrow \tan 30^\circ = \dfrac{{FC}}{{10}}\]
The tangent of the angle measuring \[30^\circ \] is equal to \[\dfrac{1}{{\sqrt 3 }}\].
Substituting \[\tan 30^\circ = \dfrac{1}{{\sqrt 3 }}\] in the expression, we get
\[ \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{{FC}}{{10}}\]
Multiplying both sides of the equation by 10, we get
\[ \Rightarrow FC = \dfrac{{10}}{{\sqrt 3 }}\]
Rationalising the denominator by multiplying and dividing the expression by \[\sqrt 3 \], we get
\[\begin{array}{l} \Rightarrow FC = \dfrac{{10}}{{\sqrt 3 }} \times \dfrac{{\sqrt 3 }}{{\sqrt 3 }}\\ \Rightarrow FC = \dfrac{{10\sqrt 3 }}{3}\end{array}\]
Thus, we get the radius of the smaller base of the frustum as \[\dfrac{{10\sqrt 3 }}{3}\] cm.
Using the formula for tangent in triangle AGE, we have
\[ \Rightarrow \tan \angle GAE = \dfrac{{GE}}{{AG}}\]
Substituting \[\angle GAE = 30^\circ \] and \[AG = 20\] cm in the equation, we get
\[ \Rightarrow \tan 30^\circ = \dfrac{{GE}}{{20}}\]
Substituting \[\tan 30^\circ = \dfrac{1}{{\sqrt 3 }}\] in the expression, we get
\[ \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{{GE}}{{20}}\]
Multiplying both sides of the equation by 20, we get
\[ \Rightarrow GE = \dfrac{{20}}{{\sqrt 3 }}\]
Rationalising the denominator by multiplying and dividing the expression by \[\sqrt 3 \], we get
\[\begin{array}{l} \Rightarrow GE = \dfrac{{20}}{{\sqrt 3 }} \times \dfrac{{\sqrt 3 }}{{\sqrt 3 }}\\ \Rightarrow GE = \dfrac{{20\sqrt 3 }}{3}\end{array}\]
Thus, we get the radius of the larger base of the frustum as \[\dfrac{{20\sqrt 3 }}{3}\] cm.
Now, we will calculate the volume of the frustum of the cone formed.
Substituting \[h = 10\] cm, \[R = \dfrac{{20\sqrt 3 }}{3}\] cm, and \[r = \dfrac{{10\sqrt 3 }}{3}\] cm in the formula for volume of the frustum,\[\dfrac{1}{3}\pi h\left( {{R^2} + {r^2} + Rr} \right)\], we get
Volume of frustum \[ = \dfrac{1}{3}\pi \times 10\left[ {{{\left( {\dfrac{{20\sqrt 3 }}{3}} \right)}^2} + {{\left( {\dfrac{{10\sqrt 3 }}{3}} \right)}^2} + \left( {\dfrac{{20\sqrt 3 }}{3}} \right)\left( {\dfrac{{10\sqrt 3 }}{3}} \right)} \right]\]
Applying the exponents on the bases, we get
\[ \Rightarrow \] Volume of frustum \[ = \dfrac{1}{3}\pi \times 10\left[ {\dfrac{{400 \times 3}}{9} + \dfrac{{100 \times 3}}{9} + \left( {\dfrac{{20\sqrt 3 }}{3}} \right)\left( {\dfrac{{10\sqrt 3 }}{3}} \right)} \right]\]
Multiplying the terms in the expression, we get
\[ \Rightarrow \] Volume of frustum \[ = \dfrac{{10}}{3}\pi \left[ {\dfrac{{400}}{3} + \dfrac{{100}}{3} + \dfrac{{200}}{3}} \right]\]
Adding the terms in the bracket, we get
\[ \Rightarrow \] Volume of frustum \[ = \dfrac{{10}}{3}\pi \left[ {\dfrac{{700}}{3}} \right]\]
Multiplying the terms in the expression, we get
\[ \Rightarrow \] Volume of frustum \[ = \dfrac{{7000}}{9}\pi \]
Now, we will calculate the volume of the cylindrical wire.
The radius of the cylinder wire is half of its diameter, that is \[r = \dfrac{d}{2}\].
Substituting \[d = \dfrac{1}{{16}}\] cm in the expression, we get
\[ \Rightarrow r = \dfrac{{\dfrac{1}{{16}}}}{2}\]
Simplifying the expression, we get
\[ \Rightarrow r = \dfrac{1}{{32}}\] cm
Let the length of the cylindrical wire be \[x\] cm.
Substituting \[h = x\] cm and \[r = \dfrac{1}{{32}}\] cm in the formula for volume of the cylindrical wire, \[\pi {r^2}h\], we get
Volume of cylindrical wire \[ = \pi \times {\left( {\dfrac{1}{{32}}} \right)^2} \times x\]
Multiplying the terms in the expression, we get
\[ \Rightarrow \] Volume of cylindrical wire \[ = \dfrac{{\pi x}}{{1024}}\]
Now, it is given that the wire is drawn out from the frustum.
This means that the metal used to make the frustum is drawn into the cylindrical wire.
Therefore, the volume of the frustum is equal to the volume of the cylindrical wire.
Therefore, we get the equation
\[ \Rightarrow \dfrac{{7000}}{9}\pi = \dfrac{{\pi x}}{{1024}}\]
This is a linear equation in terms of \[x\]. We will solve this to find the value of \[x\], and hence, the length of the cylindrical wire.
Simplifying the equation, we get
\[ \Rightarrow \dfrac{{7000}}{9} = \dfrac{x}{{1024}}\]
Multiplying both sides of the equation by 1024, we get
\[ \Rightarrow \dfrac{{7000}}{9} \times 1024 = x\]
Simplifying the expression, we get
\[ \Rightarrow x = \dfrac{{7168000}}{9}\] cm
Rewriting the expression in decimals and rounding the value, we get
\[\begin{array}{l} \Rightarrow x = 796444.44\\ \Rightarrow x \approx 796444\end{array}\]
Therefore, the value of \[x\] is 796444 cm.
This can be written as \[7964.44\] metres.
Thus, the length of the wire is approximately \[7964.44\] metres.
Note: We have not substituted \[\pi = \dfrac{{22}}{7}\] because they can get cancelled out in the equation \[\dfrac{{7000}}{9}\pi = \dfrac{{\pi x}}{{1024}}\]. Therefore, substituting the value and multiplying them earlier is not required.
We can make a mistake by using the given value \[\dfrac{1}{{16}}\] cm as radius. It is the diameter, and not radius. So, we need to divide the diameter by 2 to get the radius.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success
Master Class 11 Economics: Engaging Questions & Answers for Success
Master Class 11 Business Studies: Engaging Questions & Answers for Success
Master Class 11 Accountancy: Engaging Questions & Answers for Success
Questions & Answers - Ask your doubts
Master Class 11 Accountancy: Engaging Questions & Answers for Success
Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE
Difference Between Plant Cell and Animal Cell
Given that HCF 306 657 9 find the LCM 306 657 class 9 maths CBSE
The highest mountain peak in India is A Kanchenjunga class 9 social science CBSE
What is pollution? How many types of pollution? Define it
Differentiate between the Western and the Eastern class 9 social science CBSE