Question

A man wants to reach point B on the opposite bank of the river flowing at a speed as shown in the figure. What minimum speed relative to water should the man have so that he can reach point B?

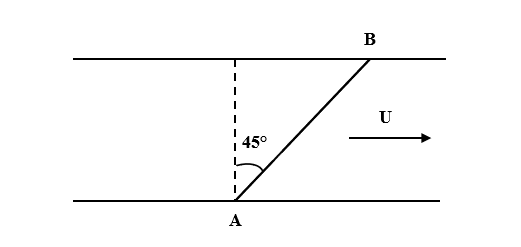
Answer 1

Hint: To solve this problem, consider V as the velocity of the man and ${V}_{B}$ as the resultant of U and V. Then, find the components of ${V}_{B}$ in X and Y axes. Then, find the relation between 45° and components of ${V}_{B}$ along X-axis and Y-axis. Substitute the values of the components and solve it to get an equation for V in terms of U. Substitute the condition for V to be minimum and find V. This will give the minimum velocity of man to reach point B.

Complete answer:
Let V be the speed of the man in still water.

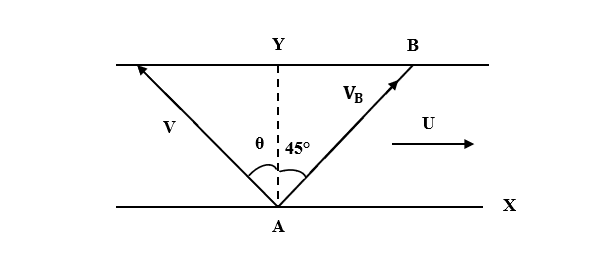
Resultant of U and V should be along AB.
Let ${V}_{B}$ be the absolute velocity of man.
Component of ${V}_{B}$ along X-axis can be given by,
${V}_{X}= U – V \sin {\theta}$ …(1)
Component of ${V}_{B}$ along Y-axis can be given by,
${V}_{Y}= V \cos {\theta}$ …(2)
In $\triangle YAB$,
$\tan {\theta}= \dfrac {Opposite \quad side}{Adjacent \quad side}$
Substituting values in above equation we get,
$\tan 45°= \dfrac {{V}_{Y}}{{V}_{X}}$
$\Rightarrow 1= \dfrac {{V}_{Y}}{{V}_{X}}$ …(3)
Substituting equation. (1) and equation. (2) in equation. (3) we get,
$1= \dfrac {V \cos {\theta}}{ U – V \sin {\theta}}$
$\Rightarrow U – V \sin {\theta}$ = $V \cos {\theta}$
$\Rightarrow U $ = $V \sin {\theta}+ V \cos {\theta}$
$\Rightarrow U $= $V (\sin {\theta}+ \cos0 {\theta})$
$\Rightarrow V $= $\dfrac {U}{\sin {\theta}+ \cos {\theta}}$ …(4)
We know, $u\sin {\theta}+v \cos {\theta} $= $ \sqrt {{u}^{2}+{v}^{2}}$
$\Rightarrow \sin {\theta}+\cos {\theta} $ = $ \sqrt {2}$
$\Rightarrow V $ = $\dfrac {U}{{\sqrt{2}}\sin {\theta+ 45°}}$ …(5)
V will be minimum at,
$\theta + 45° $= $ 90°$
$\Rightarrow \theta $ = $ 45°$
Substituting this value in the equation. (5) we get,
${ V}_{min}$ = $ \dfrac {U}{{\sqrt{2}}\sin {45°+ 45°}}$
$\Rightarrow {V}_{min} $ = $ \dfrac {U}{{\sqrt{2}}\sin 90°}$
$\Rightarrow {V}_{min} $= $ \dfrac {U}{\sqrt {2}}$
Hence, the man should have a relative speed of $ \dfrac {U}{\sqrt {2}}$ to reach point B.

Note:
If the man has to cross the river and reach the exact opposite bank of the river then the velocity of swimming of man should always be greater than the velocity of the flow of the river. If the velocity of the flow of the river is larger than the velocity of the man then the man can never reach the point exactly opposite to the bank. In this question, the man does not have to reach the exact opposite bank of the river. Hence, the velocity of swimming of the man is less than the velocity of the flow of the river.