Question

A man standing on a road has to hold his umbrella at $30^\circ $ with the vertical to keep the rain away. He throws umbrella and starts running at 10 kmph He finds that rain drops are hitting his head vertically the speed of raindrops relative to the ground is:
A) $10kmph$
B) $20kmph$
C) $10\sqrt 3 kmph$
D) $20\sqrt 3 kmph$

Answer 1

Hint:We use here the concept of relative velocity in two dimensions as we know if we want to find velocity of rain with respect to man then we have to subtract velocity of man from the velocity of rain with respect to ground. By using this relation we can calculate velocity of rain with respect to ground.

Step by step solution:
Let’s assume the velocity of rain with respect to ground is ${V_{RG}}$ which is $30^\circ $ with the vertical and velocity of man with respect to ground is given ${V_{MG}} = 10kmph$ and velocity of rain with respect to man ${V_{RM}}$ is given it is perpendicular to man
Velocity of rain with respect to ground is given $30^\circ $with the vertical, horizontal and vertical component are shown in figure

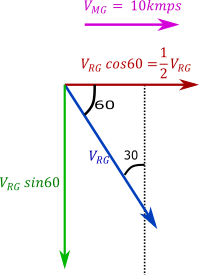
Horizontal component of velocity of rain with respect to ground is ${V_{RG}}\cos 60 = \dfrac{1}{2}{V_{RG}}$
And the vertical component is ${V_{RG}}\sin 60 = \dfrac{{\sqrt 3 }}{2}{V_{RG}}$
So we can write the velocity of rain with respect to ground in vector form $ \Rightarrow {\vec V_{RG}} = \dfrac{1}{2}{V_{RG}}\hat i - \dfrac{{\sqrt 3 }}{2}{V_{RG}}\hat j$
And velocity of man with respect to ground is ${\vec V_{MG}} = 10\hat i$
Now the velocity of rain with respect to man can find as
$ \Rightarrow {\vec V_{RM}} = {\vec V_{RG}} - {\vec V_{MG}}$
Put the value of ${\vec V_{RG}}$ and ${\vec V_{MG}}$ from above
\[ \Rightarrow {\vec V_{RM}} = \dfrac{1}{2}{V_{RG}}\hat i - \dfrac{{\sqrt 3 }}{2}{V_{RG}}\hat j - 10\hat i\]
Rearranging
\[ \Rightarrow {\vec V_{RM}} = \left( {\dfrac{1}{2}{V_{RG}} - 10} \right)\hat i - \dfrac{{\sqrt 3 }}{2}{V_{RG}}\hat j\]....................... (1)
Now in the question it is given that He finds that rain drops are hitting his head vertically its means the velocity of rain with respect to man have only vertical component $( - \hat j)$
So the horizontal component must be zero in above equation means coefficient of $\hat i$ must be zero
\[ \Rightarrow \left( {\dfrac{1}{2}{V_{RG}} - 10} \right) = 0\]
\[ \Rightarrow \dfrac{1}{2}{V_{RG}} = 10\]
Solving it
$\therefore {V_{RG}} = 20$
So we get the magnitude of velocity of rain with respect to ground is $20kmph$

Hence option B is correct

Note:By this simple concept we can solve these types of question easily in this question velocity of rain with respect to man is also asked then we can solve it in simple manner we just put the value of ${V_{RG}}$ in equation (1) and will get the answer.