Question

A man on the top of a tower standing on the seashore finds the boat coming towards him takes 10 minutes for the angle of depression to change from \[{30^ \circ }\]to \[{60^ \circ }\]. Find the time( in minutes) taken by the boat to reach the shore from his position.

Answer 1

Hint: Here we draw a rough diagram of the situation where we assume height of the tower as a variable and the distances between the tower and the boat from both angles as separate variables. Since, the tower is perpendicular to the ground, we use the concept of right triangle where we can find tan of an angle by dividing perpendicular by base of that triangle.
* Angle of depression is the angle formed between the horizontal line and line of sight. Generally an observer needs to be at a higher position than the object to have an angle of depression.

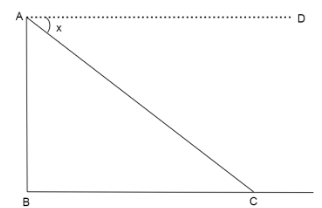
If C is an object placed at ground level and A is the point where the observer is placed then the horizontal line is AD and the line of sight is AC. So, the angle of depression formed is x.

Complete step-by-step answer:
We draw a diagram where the position of man is on top of the tower and the boat is approaching towards the seashore.

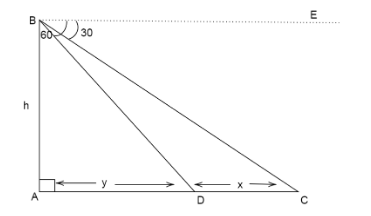
Here \[AB = h,CD = x,AD = y\]
Since the ground is perpendicular to the tower \[\angle A = {90^ \circ }\].
Since the horizontal line is parallel to the ground, using the property that when a transversal cuts two parallel lines the alternate interior angles are equal.
Here, BC cuts the set of parallel lines AC and BE then \[\angle EBC = \angle BCA = {30^ \circ }\]
Also, BD cuts the set of parallel lines AC and BE then \[\angle EBD = \angle BDA = {60^ \circ }\]
Now we know that in a right angled triangle, if one of the angles is given we can apply trigonometric function tan to the angle and write it equal to the perpendicular divided by the base of the triangle.
So, in \[\vartriangle ABC\], \[\angle C = {30^ \circ }\]
\[ \Rightarrow \tan {30^ \circ } = \dfrac{{AB}}{{AC}}\]
We can write \[AC = AD + DC\]
\[ \Rightarrow \tan {30^ \circ } = \dfrac{{AB}}{{AD + DC}}\]
Substituting the value of \[AB = h,CD = x,AD = y\]
\[ \Rightarrow \tan {30^ \circ } = \dfrac{h}{{y + x}}\]
Substitute the value of \[\tan {30^ \circ } = \dfrac{1}{{\sqrt 3 }}\]
\[ \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{h}{{y + x}}\]
Cross multiply the values from both sides
\[ \Rightarrow x + y = h\sqrt 3 \] … (1)
Similarly, in \[\vartriangle ABD\], \[\angle C = {60^ \circ }\]
\[ \Rightarrow \tan {60^ \circ } = \dfrac{{AB}}{{AD}}\]
Substitute the values of \[AB = h,CD = x,AD = y\]
\[ \Rightarrow \tan {60^ \circ } = \dfrac{h}{y}\]
Substitute \[\tan {60^ \circ } = \sqrt 3 \]
\[ \Rightarrow \sqrt 3 = \dfrac{h}{y}\]
Cross multiply the values on both sides
\[ \Rightarrow y = \dfrac{h}{{\sqrt 3 }}\] … (2)
Substitute the value of y from equation (2) in equation (1).
\[ \Rightarrow x + \dfrac{h}{{\sqrt 3 }} = h\sqrt 3 \]
Shift all values having variable h on RHS of the equation.
\[ \Rightarrow x = h\sqrt 3 - \dfrac{h}{{\sqrt 3 }}\]
Take LCM on RHS
\[ \Rightarrow x = \dfrac{{h\sqrt 3 \times \sqrt 3 - h}}{{\sqrt 3 }}\]
Put \[\sqrt 3 \times \sqrt 3 = 3\]
\[ \Rightarrow x = \dfrac{{3h - h}}{{\sqrt 3 }}\]
\[ \Rightarrow x = \dfrac{{2h}}{{\sqrt 3 }}\]
Now we are given that boat takes 10 minutes to cover the distance CD
So, we substitute the value of x as 10
\[ \Rightarrow 10 = \dfrac{{2h}}{{\sqrt 3 }}\]
Divide both sides by 2
\[ \Rightarrow \dfrac{{10}}{2} = \dfrac{{2h}}{{2\sqrt 3 }}\]
Cancel the same terms from numerator and denominator.
\[ \Rightarrow 5 = \dfrac{h}{{\sqrt 3 }}\]
We know from equation (2) \[y = \dfrac{h}{{\sqrt 3 }}\]
\[ \Rightarrow 5 = y\]
So, if the time taken by boat to cover distance CD is 10 minutes then the time taken by boat to reach the shore from that point is 5 minutes.

Note: Students are likely to make mistakes in the solution if they are unaware of the values of \[\tan {60^ \circ },\tan {30^ \circ }\]. Also, many students make an attempt to solve this question by writing the time as a product of speed and distance which is unnecessary and it will make the solution more complex.