Question

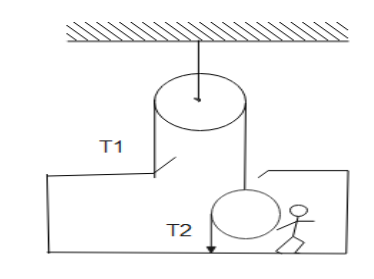
A man of mass m is inside a box of the same mass. The whole system is suspended with ideal strings and pulleys as shown in the above figure. The tension \[{{T}_{1}}\] in the string so as to keep the system in equilibrium is

Answer 1

Hint: Now let us consider the tension caused on the strings is due to the pulling and its attachment to the pulley on the top. Then by using Newton’s third law of motion which states that when an object A exerts force on object B then object B must exert a force on object A which is of equal magnitude and opposite direction. We will establish equilibrium conditions of the given system. Using this we will find the tension on the string \[{{T}_{1}}\].

Complete Step-By-Step answer:
The whole system as we can view in the diagram above is suspended with ideal strings and pulleys.
We have been given that,
The mass of the man = the mass of the box = m
The total mass will be ‘2m’ as the man is standing on the box.

Now the magnitude of the weight of the man and the box acting in the downward direction will be ‘mg’.

We can see that the second pulley shown in the diagram is an ideal pulley so we can say that the force acting on this pulley will be zero, so hence we get,
\[2{{T}_{2}}={{T}_{1}}\]……………., Taking this as equation 1,

But we know that for any given system to be in equilibrium condition the upward force and downward force must be balanced.
Therefore, we have,
\[{{T}_{1}}+{{T}_{2}}=mg+mg-{{T}_{2}}\]
\[{{T}_{1}}+2{{T}_{2}}=2mg\]

From equation 1 we have, \[2{{T}_{2}}={{T}_{1}}\], hence replacing, we get,
\[\begin{align}
  & {{T}_{1}}+{{T}_{1}}=2mg \\
 & 2{{T}_{1}}=2mg \\
 & {{T}_{1}}=mg \\
\end{align}\]

Therefore, to keep the system in equilibrium condition, the tension \[{{T}_{1}}\] in the string must be \[mg\].

Note:
Tension is a form of restoring force which has properties of pulling. However, tension comes into significance only when we consider systems consisting of strings and ropes. Adding on apart from tension we also have other restoring forces which are a part of simple harmonic motion.