Question

A line intersects the y-axis and x-axis at a point P and Q respectively. If (2,-5) is the midpoint of PQ, then find the coordinates of P and Q.

Answer 1

Hint: It is given that the line intersects the x-axis and the y-axis at a certain point. Whenever a line intersects at the x-axis then the point of intersection can be taken as (x, 0) and when it cuts the y-axis the point of intersection is taken as (0, y). Using this concept along with the basic formula of the midpoint of any two points (x, y) and (p, q) we can get the answer.

Complete step-by-step answer:

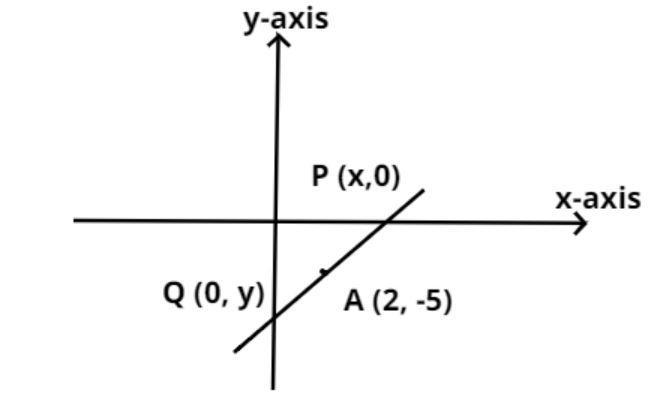
Consider the line as shown in figure it intersects the y-axis and x-axis at points P and Q respectively.
Therefore the coordinates of P is (x, 0) and the coordinates of Q is (0, y).
And it is given that the midpoint of the line is (2, -5).
As we see that in the above coordinate x is positive and y is negative therefore the line is in the fourth quadrant as in the fourth quadrant x is positive and y is negative.
Now, apply the midpoint property, if (a, b) is the midpoint of the points (e, f) and (g, h).
$ \Rightarrow a = \dfrac{{e + g}}{2},{\text{ }}b = \dfrac{{f + h}}{2}$ So, use this property we have,
As (2, -5) is the midpoint of (x, 0) and (0, y)
$ \Rightarrow 2 = \dfrac{{x + 0}}{2},{\text{ }} - 5 = \dfrac{{0 + y}}{2}$
$ \Rightarrow 4 = x + 0,{\text{ - 10}} = 0 + y$
$ \Rightarrow x = 4{\text{ & }}y = - 10$
Therefore the coordinates of P is (4, 0) and the coordinates of Q is (0, -10)
So, this is the required answer.

Note: Whenever we face such type of problems the key concept is about the understanding that any general point on x axis can be taken as (x, 0) as the y-coordinate on x axis is zero, similarly any general point on y axis can be taken as (0, y) as the x-coordinate on y-axis is zero. Having the basic idea of the midpoint formula can also help getting the right answer.