Question

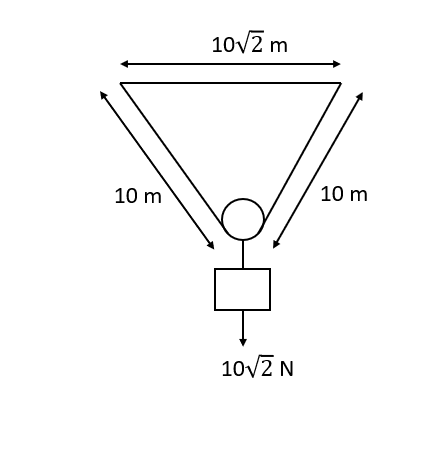
A light and inextensible string of length $L = 20 m$ tired between two nails, supports a frictionless pulley of weight $W_{p} = 10 \sqrt{2} N$ from which a block of weight $W_{b} = 10 \sqrt{2} N$ is also suspended as shown in the figure. The nails are fixed in a level a distance $x = 10 \sqrt{2} m$ apart. Radius of the pulley is $r = 10 cm$. How much normal reaction per unit of its length does the string apply on the pulley.

Answer 1

Hint: A force is acting normally on two surfaces in touch with each other. It is an estimation of the force keeping the two surfaces together. The higher the normal reaction force, the higher the value of limiting resistance. If weight is the only upward force acting on an object moving on a uniform surface, the normal reaction force is equivalent in magnitude but opposite in direction to the weight. Friction, therefore, is enhanced by increasing the weight.

Complete step-by-step solution:
Given: Radius of pulley $ = 10 cm = 0.1 m$
dl: length of arc
$d \theta = \dfrac{dl}{r}$
$dl = 0.1 d \theta$

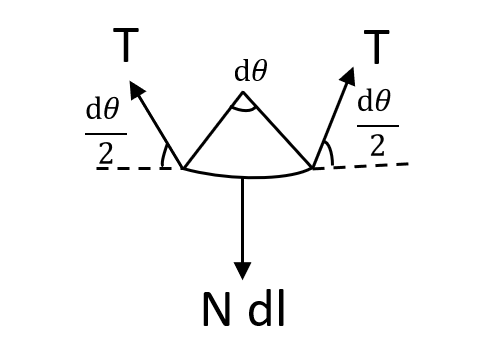
Now, we will balance the forces vertically.
$2T sin \dfrac{d \theta}{2} = N dl$
For small angle, it will become,
$2T \dfrac{d \theta}{2} = N dl$
$ T d \theta = N dl$
It will give,
$N = 10T$ ……(1)

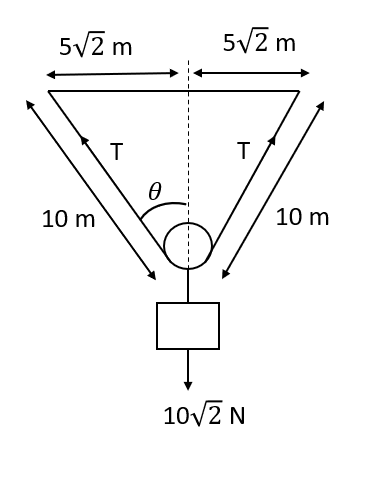
Now we will find sine of angle in the above,
$ sin \theta = \dfrac{5 \sqrt{2}}{10}$
$\implies sin \theta = \dfrac{1}{\sqrt{2}}$
It will give,
$\theta = 45^{\circ}$
Now, we will find the value of T:
$2T cos 45^{\circ} = W_{p} + W_{b}$
$\implies 2T \times \dfrac{1}{\sqrt{2}} = 20 \sqrt{2}$
$\implies T = 20 N$
Now we have to find the normal reaction by equation (1).
$ N = 10 \times 20 = 200 N$
Thus, the normal reaction per unit of its length on the pulley is $200 N$.

Note: The force holding a load is upright to the surface of touch between the load and its provider, and this force is termed a normal force, often shown with the symbol N. The word normal indicates normal to a surface. The normal force is not forever equal to the object's weight if other forces act on the object or if the object is quickening so that the whole force is not zero.