Question

A ladder rests against a wall so that its top touches the roof of the house. If the ladder makes an angle of ${60^0}$ with the horizontal and the height of the house be $6\sqrt 3 m$, then the length of the ladder is
$A)12\sqrt 3 m$
$B)12m$
$C)\dfrac{{12}}{{\sqrt 3 }}m$
$D)$ None of these

Answer 1

Hint: First, we need to know about the horizontal and vertical lines.
Let the horizontal lines are the lines that are parallel to the x-axis in the two-dimensional graph (right and left) and vertical lines are the lines parallel to the y-axis in the two-dimensional graph (bottom and top)
Since the ladder rest against a wall and its angle is given as sixty degrees and the height is given as $6\sqrt 3 m$

Complete step by step answer:
Since from the given that we have the angle and horizontal line, using these we have to find the length of the ladder.

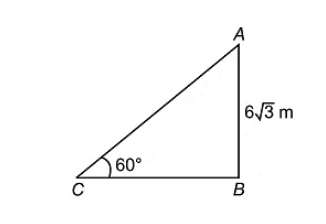
We plotted the diagram using the above information; thus, AB is the height of the given house and thus we have $AB = 6\sqrt 3 m$
We have to find the length of the ladder, so AC be the length of the ladder whose length is unknown and fix that with any variable, thus we have $AC = x$(meters)
From the ladder and house, it makes a triangle format in the diagram, and also its angle is given as ${60^0}$ for the triangle ACB, which can be represented as $\angle ACB = {60^0}$
Thus, in the right-angled triangle we know that $\vartriangle ABC \Rightarrow \dfrac{{AB}}{{AC}} = \sin \theta $ (opposite side divides the hypotenuse)
Since the angle is given as $\angle ACB = {60^0}$ and thus we get \[\dfrac{{AB}}{{AC}} = \sin {60^0}\]
Since the value of $AB = 6\sqrt 3 m$ and also the \[\sin {60^0} = \dfrac{{\sqrt 3 }}{2}\]
Hence, we get \[\dfrac{{AB}}{{AC}} = \sin {60^0} \Rightarrow AC = \dfrac{{AB}}{{\sin {{60}^0}}} \Rightarrow \dfrac{{6\sqrt 3 }}{{\dfrac{{\sqrt 3 }}{2}}}\]
Further solving the equation, we get \[AC = \dfrac{{AB}}{{\sin {{60}^0}}} \Rightarrow \dfrac{{6\sqrt 3 }}{{\dfrac{{\sqrt 3 }}{2}}} \Rightarrow 6 \times 2 \Rightarrow 12\]
Hence, we get the ladder length as $12m$

So, the correct answer is “Option B”.

Note: By using the right-angled triangle formula, we find $\vartriangle ABC \Rightarrow \dfrac{{AB}}{{AC}} = \sin \theta $
Also, by using the trigonometric value for the sine table we get \[\sin {60^0} = \dfrac{{\sqrt 3 }}{2}\]
With the help of these two pieces of information, we easily solved the given problem, as we found the required length of the ladder.