
A ladder rests against a wall at an angle $\alpha $ to the horizontal. Its foot is pulled away from the wall through a distance “a” so that it slides a distance “b” down the wall making an angle of $\beta $ with the horizontal then,
(a) $a=b\tan \dfrac{\alpha +\beta }{2}$
(b) $a=b\cot \dfrac{\alpha +\beta }{2}$
(c) $a=b\tan \dfrac{\alpha -\beta }{2}$
(d) None of the above
Answer
576k+ views
Hint: First of all draw the figure of the information given in the above question. Then apply the trigonometric ratios $\sin \theta =\dfrac{P}{H}$ and $\cos \theta =\dfrac{B}{H}$. In these trigonometric ratios that we have just shown $\theta $ is the angle, $P, B\And H$ are the perpendicular, base, and hypotenuse respectively of the right triangle with respect to angle $\theta $. Solve the equations and get the answer.
Complete step-by-step solution:
We have given that a ladder rests against a wall at an angle $\alpha $ to the horizontal. Its foot is pulled away from the wall through a distance “a” so that it slides a distance “b” down the wall making an angle of $\beta $ with the horizontal. We are drawing the above explanation as follows:
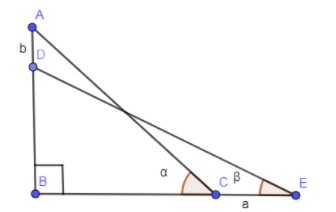
In the above figure, we have represented the original ladder position as AC, final ladder position as DE. Length of AD is “b” and length of CE is “a”. Angles $\alpha \And \beta $ are self explanatory.
Let us assume the length of the ladder as “l”. As length of the ladder remains same before and after sliding so we are going to apply $\sin \alpha $ in $\Delta ABC$ which is equal to:
We know that,
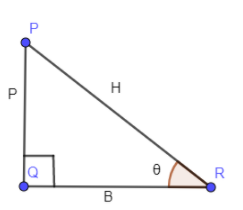
$\sin \theta =\dfrac{P}{H}$
In the above equation, P represents the perpendicular and “H” represents the hypotenuse with respect to angle $\theta $ in a right triangle.
$\cos \theta =\dfrac{B}{H}$
In the above equation, P represents the perpendicular and “H” represents the hypotenuse with respect to angle $\theta $ in a right triangle.
Now, using this $\sin \theta $ relation in $\Delta ABC$ we get,
$\sin \alpha =\dfrac{P}{H}$
In the above equation, P is equal to AB and H is equal to AC.
$\sin \alpha =\dfrac{AB}{AC}$
We have assumed length of ladder as “l” so substituting the value of AC as l we get,
$\sin \alpha =\dfrac{AB}{l}$
We can write AB as $AD+DB$ in the above equation.
$\begin{align}
& \sin \alpha =\dfrac{AD+DB}{l} \\
& \Rightarrow \sin \alpha =\dfrac{b+DB}{l} \\
\end{align}$
Cross multiplying the above equation we get,
$\begin{align}
& l\sin \alpha =b+DB \\
& \Rightarrow b=l\sin \alpha -DB......Eq.(1) \\
\end{align}$
$\begin{align}
& \cos \alpha =\dfrac{BC}{AC} \\
& \Rightarrow \cos \alpha =\dfrac{BC}{l} \\
& \Rightarrow BC=l\cos \alpha ......Eq.(2) \\
\end{align}$
Now, in $\Delta DBE$ applying trigonometric ratio of:
$\cos \beta =\dfrac{BE}{DE}$
In the above equation, DE is the length of the ladder which we have assumed as “l”.
$\begin{align}
& \cos \beta =\dfrac{BE}{l} \\
& \Rightarrow l\cos \beta =BE \\
\end{align}$
We can write BE as $BC+CE$ in the above equation.
$l\cos \beta =BC+CE$
It is given that CE equals “a” so putting the value of CE as “a” in the above equation.
\[\begin{align}
& l\cos \beta =BC+a \\
& \Rightarrow a=l\cos \beta -BC.....Eq.(3) \\
\end{align}\]
$\begin{align}
& \sin \beta =\dfrac{DB}{DE} \\
& \Rightarrow \sin \beta =\dfrac{DB}{l} \\
& \Rightarrow DB=l\sin \beta .......Eq.(4) \\
\end{align}$
Now, dividing eq. (3) by eq. (1) we get,
$\dfrac{a}{b}=\dfrac{l\cos \beta -BC}{l\sin \alpha -DB}$
Substituting the values of BC and DB from eq. (2 & 4) we get,
\[\begin{align}
& \dfrac{a}{b}=\dfrac{l\cos \beta -l\cos \alpha }{l\sin \alpha -l\sin \beta } \\
& \Rightarrow \dfrac{a}{b}=\dfrac{l\left( \cos \beta -\cos \alpha \right)}{l\left( \sin \alpha -\sin \beta \right)} \\
& \Rightarrow \dfrac{a}{b}=\dfrac{\left( \cos \beta -\cos \alpha \right)}{\left( \sin \alpha -\sin \beta \right)} \\
\end{align}\]
Now, applying the identity of $\cos C-\cos D$in the numerator and the identity of $\sin C-\sin D$ in the denominator we get,
$\begin{align}
& \cos C-\cos D=2\sin \left( \dfrac{C+D}{2} \right)\sin \left( \dfrac{D-C}{2} \right) \\
& \sin C-\sin D=2\sin \left( \dfrac{C-D}{2} \right)\cos \left( \dfrac{C+D}{2} \right) \\
\end{align}$
\[\dfrac{a}{b}=\dfrac{\left( 2\sin \left( \dfrac{\beta +\alpha }{2} \right)\sin \left( \dfrac{\alpha -\beta }{2} \right) \right)}{\left( 2\sin \left( \dfrac{\alpha -\beta }{2} \right)\cos \left( \dfrac{\alpha +\beta }{2} \right) \right)}\]
In the above equation, $2\sin \left( \dfrac{\alpha -\beta }{2} \right)$ will be cancelled out from the numerator and the denominator and then the above equation will look like:
\[\begin{align}
& \dfrac{a}{b}=\dfrac{\left( \sin \left( \dfrac{\beta +\alpha }{2} \right) \right)}{\left( cos\left( \dfrac{\alpha +\beta }{2} \right) \right)} \\
& \Rightarrow \dfrac{a}{b}=\tan \dfrac{\alpha +\beta }{2} \\
\end{align}\]
Multiplying “b” on both the sides we get,
$a=b\tan \dfrac{\alpha +\beta }{2}$
Hence, the correct option is (a).
Note: The above question demands the knowledge of trigonometric ratios and the trigonometric identities, skipping any of this information can paralyze you in this problem. And one more thing be careful in drawing the diagram of this problem, the most common problem is in the wrong demarcation of distances “a and b”. Apart from that, as the ladder’s length won’t change but if you look at the figure carefully then you will find that after sliding, it appears that ladder’s length has been increased but think logically that ladder’s length won’t change.
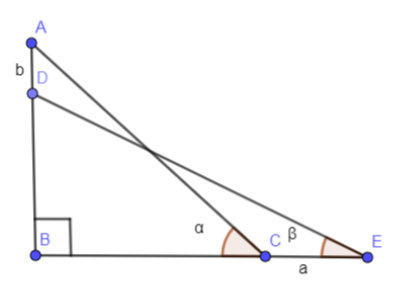
Complete step-by-step solution:
We have given that a ladder rests against a wall at an angle $\alpha $ to the horizontal. Its foot is pulled away from the wall through a distance “a” so that it slides a distance “b” down the wall making an angle of $\beta $ with the horizontal. We are drawing the above explanation as follows:

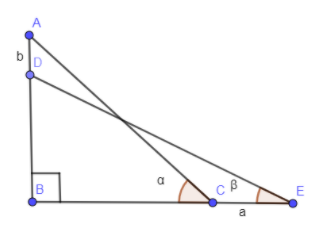
In the above figure, we have represented the original ladder position as AC, final ladder position as DE. Length of AD is “b” and length of CE is “a”. Angles $\alpha \And \beta $ are self explanatory.
Let us assume the length of the ladder as “l”. As length of the ladder remains same before and after sliding so we are going to apply $\sin \alpha $ in $\Delta ABC$ which is equal to:
We know that,
$\sin \theta =\dfrac{P}{H}$
In the above equation, P represents the perpendicular and “H” represents the hypotenuse with respect to angle $\theta $ in a right triangle.
$\cos \theta =\dfrac{B}{H}$
In the above equation, P represents the perpendicular and “H” represents the hypotenuse with respect to angle $\theta $ in a right triangle.

Now, using this $\sin \theta $ relation in $\Delta ABC$ we get,
$\sin \alpha =\dfrac{P}{H}$
In the above equation, P is equal to AB and H is equal to AC.
$\sin \alpha =\dfrac{AB}{AC}$
We have assumed length of ladder as “l” so substituting the value of AC as l we get,
$\sin \alpha =\dfrac{AB}{l}$
We can write AB as $AD+DB$ in the above equation.
$\begin{align}
& \sin \alpha =\dfrac{AD+DB}{l} \\
& \Rightarrow \sin \alpha =\dfrac{b+DB}{l} \\
\end{align}$
Cross multiplying the above equation we get,
$\begin{align}
& l\sin \alpha =b+DB \\
& \Rightarrow b=l\sin \alpha -DB......Eq.(1) \\
\end{align}$
$\begin{align}
& \cos \alpha =\dfrac{BC}{AC} \\
& \Rightarrow \cos \alpha =\dfrac{BC}{l} \\
& \Rightarrow BC=l\cos \alpha ......Eq.(2) \\
\end{align}$
Now, in $\Delta DBE$ applying trigonometric ratio of:

$\cos \beta =\dfrac{BE}{DE}$
In the above equation, DE is the length of the ladder which we have assumed as “l”.
$\begin{align}
& \cos \beta =\dfrac{BE}{l} \\
& \Rightarrow l\cos \beta =BE \\
\end{align}$
We can write BE as $BC+CE$ in the above equation.
$l\cos \beta =BC+CE$
It is given that CE equals “a” so putting the value of CE as “a” in the above equation.
\[\begin{align}
& l\cos \beta =BC+a \\
& \Rightarrow a=l\cos \beta -BC.....Eq.(3) \\
\end{align}\]
$\begin{align}
& \sin \beta =\dfrac{DB}{DE} \\
& \Rightarrow \sin \beta =\dfrac{DB}{l} \\
& \Rightarrow DB=l\sin \beta .......Eq.(4) \\
\end{align}$
Now, dividing eq. (3) by eq. (1) we get,
$\dfrac{a}{b}=\dfrac{l\cos \beta -BC}{l\sin \alpha -DB}$
Substituting the values of BC and DB from eq. (2 & 4) we get,
\[\begin{align}
& \dfrac{a}{b}=\dfrac{l\cos \beta -l\cos \alpha }{l\sin \alpha -l\sin \beta } \\
& \Rightarrow \dfrac{a}{b}=\dfrac{l\left( \cos \beta -\cos \alpha \right)}{l\left( \sin \alpha -\sin \beta \right)} \\
& \Rightarrow \dfrac{a}{b}=\dfrac{\left( \cos \beta -\cos \alpha \right)}{\left( \sin \alpha -\sin \beta \right)} \\
\end{align}\]
Now, applying the identity of $\cos C-\cos D$in the numerator and the identity of $\sin C-\sin D$ in the denominator we get,
$\begin{align}
& \cos C-\cos D=2\sin \left( \dfrac{C+D}{2} \right)\sin \left( \dfrac{D-C}{2} \right) \\
& \sin C-\sin D=2\sin \left( \dfrac{C-D}{2} \right)\cos \left( \dfrac{C+D}{2} \right) \\
\end{align}$
\[\dfrac{a}{b}=\dfrac{\left( 2\sin \left( \dfrac{\beta +\alpha }{2} \right)\sin \left( \dfrac{\alpha -\beta }{2} \right) \right)}{\left( 2\sin \left( \dfrac{\alpha -\beta }{2} \right)\cos \left( \dfrac{\alpha +\beta }{2} \right) \right)}\]
In the above equation, $2\sin \left( \dfrac{\alpha -\beta }{2} \right)$ will be cancelled out from the numerator and the denominator and then the above equation will look like:
\[\begin{align}
& \dfrac{a}{b}=\dfrac{\left( \sin \left( \dfrac{\beta +\alpha }{2} \right) \right)}{\left( cos\left( \dfrac{\alpha +\beta }{2} \right) \right)} \\
& \Rightarrow \dfrac{a}{b}=\tan \dfrac{\alpha +\beta }{2} \\
\end{align}\]
Multiplying “b” on both the sides we get,
$a=b\tan \dfrac{\alpha +\beta }{2}$
Hence, the correct option is (a).
Note: The above question demands the knowledge of trigonometric ratios and the trigonometric identities, skipping any of this information can paralyze you in this problem. And one more thing be careful in drawing the diagram of this problem, the most common problem is in the wrong demarcation of distances “a and b”. Apart from that, as the ladder’s length won’t change but if you look at the figure carefully then you will find that after sliding, it appears that ladder’s length has been increased but think logically that ladder’s length won’t change.

Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
The shortest day of the year in India

State and prove the Pythagoras theorem-class-10-maths-CBSE

A Gulab jamun contains sugar syrup up to about 30 of class 10 maths CBSE

What is UltraEdge (Snickometer) used for in cricket?

What are the public facilities provided by the government? Also explain each facility

Distinguish between the reserved forests and protected class 10 biology CBSE




