Question

A ladder reaches a wall up to a height of $ 15cm $ and the foot of the ladder is $ 8cm $ away from the base of the wall. Find the length of the ladder.

Answer 1

Hint: When a ladder is placed against a wall, the right angle triangle is formed of having two sides, whose third side can be calculated by using Pythagora's theorem
Pythagoras Theorem which states that: $ {\left( {Hyp.} \right)^2} = {\left( {Perp.} \right)^2} + {\left( {Base} \right)^2} $

Complete step-by-step answer:
We know that when a ladder is placed against a wall a right angle triangle will be formed. In the right triangle ladder act as hypotenuse and height of the wall up to which ladder reaches act as length of perpendicular of triangle and distance between foot of ladder and wall will act as length of the base of the right triangle.

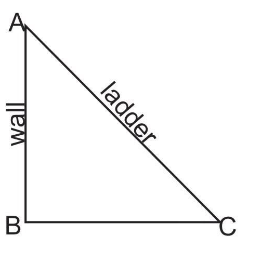
Let length of the ladder is = $ x\,cm $
Therefore, length of hypotenuse of right triangle is = $ x\,cm $
Height up to which ladder reaches the wall is $ 15cm $
Therefore, length of perpendicular of right triangle is = $ 15cm $
Distance between wall and foot of ladder is = $ 8cm $
Therefore, base of right angle triangle is $ 8cm $
Using Pythagoras theorem in the right angle triangle. Which states that:
 $ {\left( {Hyp.} \right)^2} = {\left( {Perp.} \right)^2} + {\left( {Base} \right)^2} $
Substituting values in above formula and then simplifying it for value of ‘x’.
 $
  {\left( x \right)^2} = {\left( {15} \right)^2} + {\left( 8 \right)^2} \\
   \Rightarrow {x^2} = 225 + 64 \\
   \Rightarrow {x^2} = 289 \\
   \Rightarrow {x^2} = {\left( {17} \right)^2} \\
   \Rightarrow x = 17 \\
  $
Therefore, the length of ladder is $ 17cm. $

Note: In right angle triangle problem students must very carefully study statements to understand which sides will be taken as hypotenuse, perpendicular and base while using Pythagoras theorem.