Question

A ladder 15 m long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, find the height of the wall.

Answer 1

Hint: Here, draw a figure using statements given in question. Use a trigonometric tool, sine of the angle given in the question, to find the height of the wall with the help of the length of ladder and angle given. Simplify the equation obtained and find the height of the wall.

Complete step-by-step answer:
Let AC be the ladder of length 15 m, AB be the wall. Now ∠ B = 90° and ∠ C = 60°.

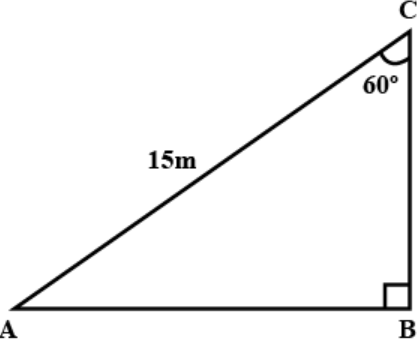
In triangle ABC,
 \[\Rightarrow \sin {30^ \circ } = \dfrac{{AB}}{{AC}}\]
[Sine is taken as it include one known side and one unknown side which we want to find]
Given, AC = 15 m
 \[\Rightarrow \dfrac{1 }{2} = \dfrac{{AB}}{{15}}\]
 $ \Rightarrow AB = \dfrac{15}{2}$
 \[\Rightarrow AB = {15 \times 0.5} = \dfrac {15}{2}\]
Thus, height of wall is 7.5 m
So, the correct answer is “7.5 m”.

Note: In these types of questions, draw the appropriate figure as per conditions given in question. Whenever we have a right angle in a triangle we can use the trigonometry concept to find the unknown length. Here in this case, the angle between bases of the line joining bases of the ladder and wall and the height of the wall is 90°, so we can easily apply the trigonometric concept. While using trigonometric tools, choose that ration which includes the length of one given side and unknown side as we know the value of sin 60° in this question.