Question

What is a jump discontinuity of a graph?

Answer 1

Hint: The solution for this question is in the descriptive way, we come across different kinds of discontinuities, but here in this question we have to explain or discuss the Jump discontinuity in detailed way and taking an example and plotting a graph for the example we can have a complete picture of a jump discontinuity.

Complete step-by-step answer:
Jump Discontinuity is a classification or type of discontinuities in which the function jumps, or steps, from one point to another along the curve of the function, often splitting the curve into two separate sections. While continuous functions are often used within mathematics, not all functions are continuous. The point on the domain of a function that is discontinuous is called the discontinuity.
A jump discontinuity occurs when the right-hand and left-hand limits exist but are not equal.
Consider an Example of a function with a jump discontinuity:
The discontinuous function \[f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}
  {x + 1} \\
  { - x}
\end{array}\,\,\,\,\,\,\begin{array}{*{20}{c}}
  {x > 0} \\
  {x \geqslant 0}
\end{array}} \right.\]
For \[x > 0\],
\[ \Rightarrow \,\,\,\mathop {\lim }\limits_{x \to 0} f\left( x \right) = \mathop {\lim }\limits_{x \to 0} \left( {x + 1} \right)\]
\[ \Rightarrow \,\,\,\mathop {\lim }\limits_{x \to 0} f\left( x \right) = 0 + 1\]
\[ \Rightarrow \,\,\,\mathop {\lim }\limits_{x \to 0} f\left( x \right) = 1\]
But, for \[x = 0\]
\[ \Rightarrow \,\,f\left( 0 \right) = 0\] (Therefore, f is continuous from the left at 0, but not the right.)
Here, in this example in which \[\mathop {\lim }\limits_{x \to {0^ + }} \] exists, and \[\mathop {\lim }\limits_{x \to {0^ - }} \] also exists, but they are not equal.
The graphical representation of above example is:

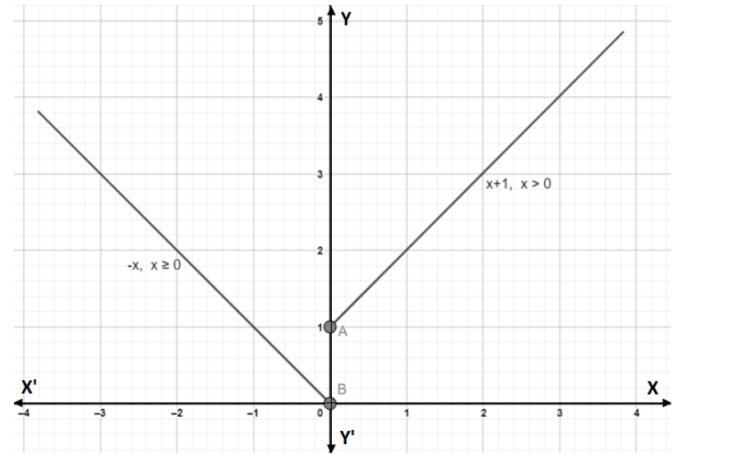
Jump discontinuities are also called "discontinuities of the first kind". These kinds of discontinuities are big breaks in the graph, but not breaks at vertical asymptotes (those are specifically called infinite or essential discontinuities). You’ll often see jump discontinuities in piecewise-defined functions. A function is never continuous at a jump discontinuity, and it’s never differentiable there, either.

Note: In this question they have mentioned about the jump discontinuity, suppose if they given any other discontinuity like infinite discontinuity, removable discontinuity, end point discontinuity or mixed continuity these are all the types of discontinuities we have to explain each type of discontinuities, by giving an suitable example it’s better to explain or understand.