Question

A jeep runs along the curve of radius $0.3km$ at constant speed of $60m{s^{ - 1}}$. The resultant change in velocity, instantaneous acceleration and average acceleration over a ${60^ \circ }$ arc is:

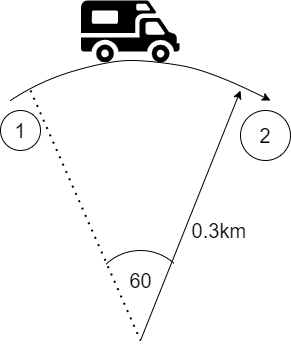
A.$30m{s^{ - 1}},11.5m{s^{ - 2}},12m{s^{ - 2}}$
B.$60m{s^{ - 1}},12m{s^{ - 2}},11.5m{s^{ - 2}}$
C.$60m{s^{ - 1}},11.5m{s^{ - 2}},12m{s^{ - 2}}$
D.$40m{s^{ - 1}},10m{s^{ - 2}},8m{s^{ - 2}}$

Answer 1

Hint: Recall the concept of velocity and acceleration of a moving body. Velocity is defined as the rate of change of displacement with time. It has both magnitude and direction. So it is a vector quantity. Acceleration is the rate of change of velocity with time. It is also a vector quantity.

Complete answer:
Step I:
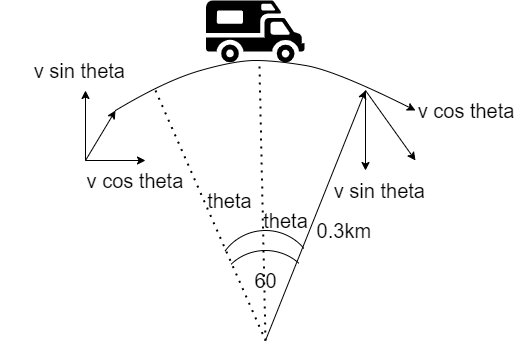
The vehicle is moving from point $1$ to point $2$. When it starts from point $1$, its velocity will be $v = 60m{s^{ - 1}}$ and the horizontal component will be $v\cos \theta $while the vertical component is $v\sin \theta $.
When it reaches point $2$, its velocity will have the same magnitude but it will point in a downward direction. So the horizontal component will be $v\cos \theta $ and the vertical component is $v\sin \theta $.

Step II:
From point $1$ to point $2$, the direction of the horizontal component of velocity is the same, but the direction of the vertical component has changed.
Therefore, the resultant change in velocity is given by
$\Delta v = 2v\sin \theta $
Given $\theta = {60^ \circ }$, but since the curve is divided in two equal parts, so \[\theta = {30^ \circ }\]
Substituting the given values,
$\Delta v = 2 \times 60 \times \sin {30^ \circ }$

$\Delta v = 2 \times 60 \times \dfrac{1}{2}$
$\Delta v = 60m{s^{ - 1}}$
Step III:
Instantaneous acceleration is the centripetal acceleration while the jeep moves towards the curve. It is given by
${a_c} = \dfrac{{{v^2}}}{R}$
Given radius $r = 0.3km = 300m$
Also the velocity is constant, so it remains the same. Substituting the values and evaluating value of acceleration,
${a_c} = \dfrac{{60 \times 60}}{{300}}$
${a_c} = 12m{s^{ - 2}}$
Step IV:
Also the average acceleration is the rate of change of velocity with time. So it is written as
${a_{avg}} = \dfrac{{\Delta v}}{{\Delta t}}$---(i)
Change in velocity is already calculated above.
It is known that $Speed = \dfrac{{Dis\tan ce}}{{Time}}$---(ii)
Therefore, $Time = \dfrac{{Dis\tan ce}}{{Speed}}$---(iii)
$Dis\tan ce = r \times \theta $
The value of $r = 0.3km = 300m$
$\theta = {60^ \circ }$. It can be written as $\dfrac{\pi }{3}$
Step V:
Therefore equation (iii) becomes,
$Time = \dfrac{{300 \times \dfrac{\pi }{3}}}{{60}}$
Average acceleration becomes,
${a_{avg}} = \dfrac{{60}}{{\dfrac{{300 \times \dfrac{\pi }{3}}}{{60}}}}$
${a_{avg}} = \dfrac{{60 \times 60}}{{100\pi }}$
${a_{avg}} = \dfrac{{3600}}{{100\pi }}$
${a_{avg}} = 11.46 \approx 11.5m{s^{ - 2}}$
Step VI:
The resultant change in velocity is $60m{s^{ - 1}}$
Instantaneous acceleration is $12m{s^{ - 2}}$
Average acceleration is $11.5m{s^{ - 2}}$

Therefore Option B is the correct answer.

Note:
Though both instantaneous and average acceleration are types of acceleration, they are different. Average acceleration is the average velocity per unit time whereas instantaneous velocity is the rate of change of velocity at a particular instant of time. The instantaneous acceleration is the term related to centripetal acceleration.