Question

A hollow sphere of external and internal diameters of $8$ cm and $4$cm respectively is melted and made into another solid in the shape of a right circular cone of base diameter $8$ cm. Find the height of the cone.

Answer 1

Hint: Here, the volume of the material in the hollow sphere will be$ = \dfrac{4}{3}\pi \left( {{{\text{R}}^3}{\text{ - }}{{\text{r}}^3}} \right)$ where R is external radius and r is internal radius. This sphere is melted into the shape of a cone. We know the Volume of Cone$ = \dfrac{1}{3}\pi \left( {{\text{Radiu}}{{\text{s}}^2}} \right) \times {\text{h}}$ where h= the height of cone. The volumes of both shapes will be equal as one is melted into another. Put the values and solve for h.

Complete step-by-step answer:
Given, The external diameter of hollow sphere=$8$cm and internal diameter of hollow sphere=$4$cm. Since radius is half of the diameter, then
$ \Rightarrow $ External radius (R) of hollow sphere$ = \dfrac{8}{2} = 4{\text{cm}}$
$ \Rightarrow $ Internal radius (r) of hollow sphere$ = \dfrac{4}{2} = 2{\text{cm}}$
We know that the volume of hollow sphere$ = \dfrac{4}{3}\pi \left( {{{\text{R}}^3}{\text{ - }}{{\text{r}}^3}} \right)$where R=external radius and r= internal radius. So, on putting the value of R and r we get,
Volume of Hollow sphere$ = \dfrac{4}{3}\pi \left( {{4^3}{\text{ - }}{{\text{2}}^3}} \right)$
On simplifying, we get
$ \Rightarrow {\text{Volume of sphere = }}\dfrac{4}{3}\pi \left( {{\text{64 - 8}}} \right) = \dfrac{{4 \times 56}}{3}\pi $ ---- (i)
This hollow sphere is melted into a right circular cone of base diameter $8$cm. Then, the radius of the cone=$\dfrac{8}{2} = 4{\text{cm}}$ .

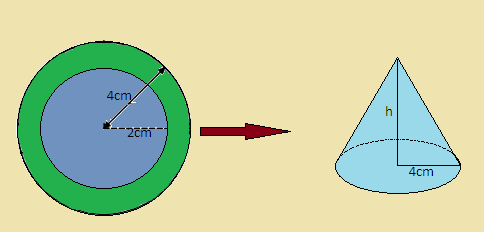
Now we know that the volume of cone $ = \dfrac{1}{3}\pi \left( {{\text{Radiu}}{{\text{s}}^2}} \right) \times {\text{h}}$ where h is height of the cone. We have to find this height. Now on putting value of radius of cone in the formula, we get-
Volume of cone=$ = \dfrac{1}{3}\pi \left( {{4^2}} \right) \times {\text{h = }} = \dfrac{{16{\text{h}}}}{3}\pi $ ---- (ii)
Since the shape of the hollow sphere is changed into the shape of the cone then the volumes of both shapes will be equal. So, Volume of cone= Volume of the hollow sphere
$ \Rightarrow \dfrac{{4 \times 56}}{3}\pi = \dfrac{{16{\text{h}}}}{3}\pi \Rightarrow 16{\text{h = }}4 \times 56$
On solving, we get
$ \Rightarrow {\text{h = }}\dfrac{{4 \times 56}}{{16}} = \dfrac{{56}}{4} = 14{\text{cm}}$
So, the height of the cone is $14$ cm.

Note: The concept we follow to solve in this question is that if one solid shape is melted and converted into another solid shape then the volume of the shape being converted is equal to the volume of shape into which it is converted.