Question

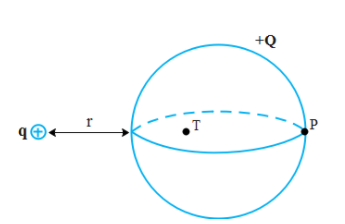
A hollow conducting sphere has a net charge of +Q. A smaller point charge +q is located at a distance r from the left side of the hollow sphere. Point P is located on the right side of the hollow sphere and point T is located somewhere on the inside of the hollow sphere not necessarily at the centre. What happens to charge density on the hollow sphere at point P and to the electric field at point T as the charge +q is brought closer to the hollow sphere?

a) The charge density at P increases and the electric field at T remains zero
b) The charge density at P remains zero and the electric field at T remains zero
c) The charge density at P increases. The electric field at T increases in magnitude and always points to the right
d) The charge density at P increases and the electric field at T remains zero
e) the charge density at P remains constant but non zero. The electric field at T remains constant, but points to the left

Answer 1

Hint: In the above figure the charge +q is at a sufficient distance to have its influence on the sphere. Let us say the charge +Q is uniformly distributed on the sphere. When the charge +q is actually present at its position it will move the charges on the charges on the sphere away from it as the charges are similar in nature i.e. repel. From this information we will arrive at a conclusion that what will happen to the net charge density of the sphere and using Gauss law we will see that the charge +q affect the electric field at point T.

Complete step-by-step answer:

In the figure 1 above a shell comprises a uniform positive charge on its surface. When a positively charged rod is brought close to it, the charge density moves on the other side due to electrostatic repulsion. This above process is called electrostatic induction.
A similar thing will take place when positive charge is kept at a distance r from the left side of the sphere. The charge density will shift towards the right of the sphere. Hence we can conclude that the charge density at point P will increase.
Now let us analyze the electric field at point T. For that let us say we enclose a Gaussian surface enclosing the inside the sphere such that the point T passes through the Gaussian surface. Hence by gauss law i.e. $\text{E}\text{. }\!\!\Delta\!\!\text{ S=}\dfrac{\text{q}}{{{\in }_{\circ }}}$ where E is the electric field on the Gaussian surface, $\Delta S$ is the surface area of the Gaussian surface, q is the charge enclosed within the surface and ${{\in }_{\circ }}$is the permittivity of free space. There is no charge present within the sphere. Hence q enclosed is zero which implies the electric field on the Gaussian surface is zero. This implies that the electric field at point P is also zero since point P lies on the Gaussian surface.
Hence we can conclude that the surface charge density at point P increases and the electric field at point T will remain zero. Hence the correct answer is option d.

Note: It is to be noted that the change in charge density does not affect the electric field inside. If the distance r was very huge then there would not be any induction and the surface density at point P would have remained the same. If the charge +q is replaced by-q then the charge density would have shifted towards the left of the sphere and hence the charge density at point P would have decreased.