Question

A hemispherical vessel of radius 14 cm is fully filled with sand. This sand is poured on a level ground. The heap of sand forms a cone shape of height 7 cm. Calculate the area of the ground occupied by the circular base of the heap of the sand.

Answer 1

Hint: To solve this question, we should know the basic formulas for the volume of a hemisphere, that is, $\dfrac{2}{3}\pi {{r}^{3}}$ and volume a cone, which is, $\dfrac{1}{3}\pi {{r}^{2}}h$ and we should also know the formula of the area of a circle too, that is $\pi {{r}^{2}}$. As per the conditions given in the question, the volume of the hemisphere is equal to the volume of the cone, so we will use this relation to find the radius of the cone and then find the base of the cone, which is a circle.

Complete step-by-step answer:

It is given in the question that a hemispherical vessel of radius 14 cm is fully filled with sand and this sand is poured on a level ground. The heap of sand forms a cone shape of height 7 cm. We have been asked to calculate the area of the ground occupied by the circular base of the heap of the sand. We can represent the conditions given in the question as in the figure below.

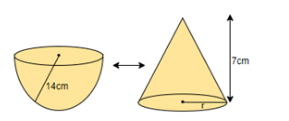
We can say that the volume of the hemisphere is exactly equal to the volume of the cone as both will contain the same amount of sand. Now, we know that the volume of a hemisphere is given by, $\dfrac{2}{3}\pi {{r}^{3}}$ and the volume of the cone is given by $\dfrac{1}{3}\pi {{r}^{2}}h$. As it is mentioned in the question that the volume of the hemisphere is equal to the volume of the cone, we can equate them. So, we will consider the radius of the hemisphere as ${{r}_{1}}$ and that of the cone as ${{r}_{2}}$. So, we will get,
$\begin{align}
  & \dfrac{2}{3}\pi {{r}_{1}}^{3}=\dfrac{1}{3}\pi {{r}_{2}}^{2}h \\
 & \Rightarrow 2\pi {{r}_{1}}^{3}=\pi {{r}_{2}}^{2}h \\
\end{align}$
We know that the radius of the hemisphere, ${{r}_{1}}=14cm$ and height of the cone, $h=7cm$. So, we will put these values in the above equality and get,
$\begin{align}
  & 2\pi \times {{\left( 14 \right)}^{3}}=\pi {{r}_{2}}^{2}\left( 7 \right) \\
 & \Rightarrow {{r}_{2}}^{2}=\dfrac{2\times \pi \times 14\times 14\times 14}{\pi \times 7} \\
 & \Rightarrow {{r}_{2}}^{2}=4\times 196 \\
 & \Rightarrow {{r}_{2}}^{2}=784 \\
 & \Rightarrow {{r}_{2}}=\sqrt{784} \\
 & \Rightarrow {{r}_{2}}=28 \\
\end{align}$
So, we get the ${{r}_{2}}$ or the radius of the cone as 28 cm. We know that the base of a cone is of a circular shape, so the area of the base of the cone will be $\pi {{r}^{2}}$. We know that the radius is 28 cm, so the area is,
$\begin{align}
  & =\dfrac{22}{7}\times 28\times 28 \\
 & \Rightarrow 22\times 4\times 28 \\
 & \Rightarrow 2,464c{{m}^{2}} \\
\end{align}$
Hence, the area of the ground occupied by the circular base of the heap of the sand is $2,464c{{m}^{2}}$.

Note: There is a chance of getting the radius of the hemisphere and the radius of the cone mixed up while equating the volume of the hemisphere and the volume of the cone. So, it is better to consider them as ${{r}_{1}}$ and ${{r}_{2}}$. This would lead to a clarity and we will be able to find the radius of the cone easily without any confusion. The students should also remember the basic volume and area formulas of the hemisphere, cone and circle.