Question

A hemispherical bowl is made up of stone whose thickness is 5cm. If the inner radius is 35 cm then find the total surface area of the bowl.

Answer 1

Hint- To solve these types of questions, we need to examine the total surface area of the bowl. As the bowl is made of stone which is 5 cm thick, so there are 2 hemispheres one is outer and the other one is inner. Also, we will have to add the area of the thickness which is visible on the top.

Complete step-by-step solution -
So, if we examine the diagram carefully, there are two hemispheres. One of them is inner and the other one is outer hemisphere.

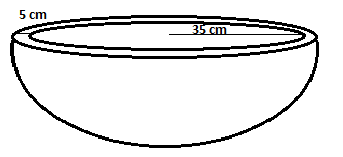
The radius of the inner Hemisphere is given in the question and is equal to 35 cm.
The bowl is made of stone which is 5 cm thick so the outer radius will have radius equal to
$
  \therefore {\text{ outer radius = inner radius + thickness}} \\
   \Rightarrow {\text{ outer radius = 35 + 5 = 40 cm}} \\
$
Now, we have to calculate the total surface area of the bowl.
The total surface area of the bowl includes the outer surface area of the bowl, the inner surface area of the bowl and the area of the thickness of the bowl that is
${\text{total surface area = surface area of outer bowl + surface area of inner bowl + area of the thickness}}$
Now, firstly we will calculate the outer surface area of the bowl
Outer radius of the bowl is
R= 40cm.
Surface area of the outer bowl=$(4\pi {R^2})/2$
$ = 2\pi {R^2}$
Inner radius of the bowl is
r= 35cm
Surface area of the inner bowl =$(4\pi {r^2})/2$
$ = 2\pi {r^2}$
Now, we have to calculate the area of the ring of thickness 5cm and the area of the ring is
$\pi ({R^2} - {r^2})$
\[\] Total surface area=surface area of outer bowl + surface area of inner bowl +area of the thickness
$ = 2\pi {R^2} + 2\pi {r^2} + \pi ({R^2} - {r^2})$
$ = \pi (2{R^2} + 2{r^2} + {R^2} - {r^2})$
$ = \pi (3{R^2} + {r^2})$
$ = \pi ((3*{(40)^2}) + {(35)^2})$
$ = 18,935.71{\text{ }}c{m^2}{\text{ using }}\pi {\text{ = 22/7}}$

Note- The main point here on which we have to focus is to include the area of the thickness of the bowl which also is visible on the top. In these types of questions, we have to calculate the area which is visible. For example in a bowl, the outer area of the bowl as well the inner area and the area of the thickness as we have solved in the above question.