Question

A heavy particle hanging from a string of length $l$ is projected horizontally with speed \[\sqrt {gl} \]. The speed of a particle at the point where the tension in the string equals weight of the particle is ?

Answer 1

Hint: Find the equation of motion of the particle and use the conservation of mechanical energy at starting point and at the point of the balance condition. From there find the speed of the particle at the point where the tension in the string is equal to the weight of the particle.

Formula used:
Newton's second law is given by,
\[F = ma\]
where \[m\] is the mass of the particle and \[a\] is the acceleration of the particle.
The conservation of mechanical energy is given by,
\[{K_i} + {U_i} = {K_f} + {U_f}\]
where, \[{K_i}\] and \[{U_i}\] are the initial kinetic and potential energy and \[{K_f},{U_f}\] are the final kinetic and potential energy.

Complete step by step answer:
We have given here that the particle is given a velocity of \[\sqrt {gl} \] horizontally. Now, the particle will start swinging due to this. So, we have to find the velocity of the particle when the weight of the particle will be equal to the tension in the string. Now, there are two forces acting on the particle vertically one is the centrifugal force and another is the gravitational pull on the particle. Let, the mass of the particle is $m$.

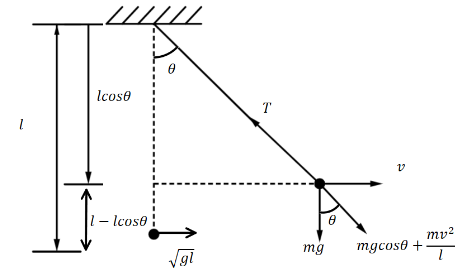
So, the equation of motion of the particle along the wire can be written as, \[T = mg\cos \theta + \dfrac{{m{v^2}}}{l}\]
Now, according to the question this is equal to the weight of the particle hence we can write,
\[mg = mg\cos \theta + \dfrac{{m{v^2}}}{l}\]….(i)
Now, from conservation of mechanical energy we can write,
\[\dfrac{1}{2}m{(\sqrt {gl} )^2} = mgl' + \dfrac{1}{2}m{(v)^2}\]
Now, from the diagram we can see that, \[l' = l - l\cos \theta \].
So, putting this value we have,
\[\dfrac{1}{2}mgl = mgl(1 - \cos \theta ) + \dfrac{1}{2}m{(v)^2}\]
\[\Rightarrow \dfrac{1}{2}mgl - mgl = - mgl\cos \theta + \dfrac{1}{2}m{(v)^2}\]

Upon simplifying we have,
\[gl\cos \theta = \dfrac{1}{2}({v^2} + gl)\]
\[\Rightarrow \cos \theta = \dfrac{1}{{2gl}}({v^2} + gl)\]…….(ii)
Putting these value in equation (i) we have,
\[mg = mg\cos \theta + \dfrac{{m{v^2}}}{l}\]
\[\Rightarrow mg = mg\dfrac{1}{{2gl}}({v^2} + gl) + \dfrac{{m{v^2}}}{l}\]
\[\Rightarrow g = \dfrac{1}{{2l}}({v^2} + gl) + \dfrac{{{v^2}}}{l}\]
Upon simplifying we have,
\[g = \dfrac{{{v^2}}}{{2l}} + \dfrac{g}{2} + \dfrac{{{v^2}}}{l}\]
\[\Rightarrow g - \dfrac{g}{2} = \dfrac{{3{v^2}}}{{2l}}\]
\[\Rightarrow {v^2} = \dfrac{{gl}}{3}\]
\[\therefore v = \sqrt {\dfrac{{gl}}{3}} \]
Hence, the speed of a particle at the point where the tension in the string equals weight of the particle is \[\sqrt {\dfrac{{gl}}{3}} \].

Note: The point at which the particle starts swinging the weight of the particle may seem equal to the tension in the string. But, at the point of starting the particle has acceleration acting in the horizontal direction and since the tension and the weight of the particle is not equal it has some motion along the vertical along with the horizontal line also.