Question

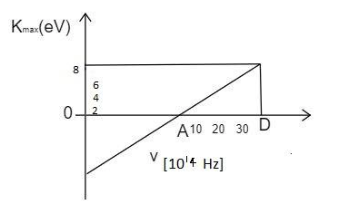
A graph regarding photoelectric effect is shown between the maximum kinetic energy of electrons and the frequency of the incident light . On the basis of the data as shown in the graph, calculate the work function.

(A) $4\,eV$
(B) $2\,eV$
(C) $4.2\,eV$
(D) $2.5\,eV$

Answer 1

Hint:Find the threshold frequency from the graph. Use the formula of the Planck’s constant and substitute the known parameters to find the value of the Planck’s constant. Substitute this value and the threshold frequency in the formula of the work function formula, to find the value of the work function.

Useful formula:
(1) The formula of the Planck’s constant is given by

$h = \dfrac{{\Delta {K_{\max }}}}{{\Delta v}}$

Where $h$ is the Planck’s constant, $\Delta {K_{\max }}$ is the change in the kinetic energy and $\Delta v$ is the change in the frequency

(2) The formula of the work function is given as

$w = h{v_0}$

Where $w$ is the work function, ${v_0}$ is the threshold frequency.

Complete step by step solution:
Analyze the graph completely,
From the graph, it is clear that the threshold frequency is ${v_0} = 10 \times {10^{14}}\,Hz$.
Using the formula of the Planck’s constant, we get

$h = \dfrac{{\Delta {K_{\max }}}}{{\Delta v}}$

Substituting the known values and converting the unit of the electron volts into Joules by multiplying it with $1.6 \times {10^{ - 19}}$ ,

$h = \dfrac{{8 \times 1.6 \times {{10}^{ - 19}}}}{{\left( {30 - 10} \right) \times {{10}^{14}}}}$

By simplifying the above equation, we get

$h = 6.4 \times {10^{ - 34}}\,J$

In order to calculate the work function, use the formula of the work function,

$w = h{v_0}$

Substituting the values of the Planck's constant and the threshold frequency, we get

$w = 6.4 \times {10^{ - 34}} \times 10 \times {10^{14}}$

By performing the basic arithmetic operation, we get

$w = 4\,eV$

Hence the work function from the given graph is $4\,eV$ .

Thus the option (A) is correct.

Note:The unit conversion from the electron volt to the Joules is made by multiplying it with $1.6 \times {10^{ - 19}}$ . The frequency of the $10 \times {10^{14}}\,Hz$ is the minimum frequency that produces the photoelectric effect. This part lies above the horizontal axis of the graph.