
A golf ball has a diameter equal to $4.1cm$. Its surface has $150$ dimplets each of radius $2mm$. Calculate total surface area which is exposed to the surroundings assuming that the dimples are hemispherical.
Answer
603.9k+ views
Hint: In this question we will use some important formulae for finding the surface area of the spherical golf ball. Here, we have given some parameters we will use them to find out the total surface area of that golf ball by using the formula:
Surface area of a sphere = $4\pi {r^2}$. And then we will remove the area of each dimplet from the total surface area.
Complete step-by-step answer:
Given that, diameter of golf ball = $4.1cm$
$ \Rightarrow {\text{ radius of the ball = }}\dfrac{{diameter}}{2} = \dfrac{{4.1}}{2}cm$
Radius of each dimplet = $2mm = \dfrac{2}{{10}}cm$.
We have,
$ \Rightarrow $ Surface area of the golf ball = $4\pi {r^2}$
$ \Rightarrow $ Surface area of the golf ball = $4 \times \pi \times {\left( {\dfrac{{4.1}}{2}} \right)^2} = 16.81\pi c{m^2}$ .
Here, there are a total of 150 dimplets present on the surface of the golf ball. Each dimplet occupies some area.
In case of each dimple, surface area is equals to $\pi {r^2}$ ( where r is the radius of each dimple ) is removed from the total surface area of the golf ball where as the surface area of the hemisphere i.e. $2\pi {r^2}$ is exposed from the surroundings.
So, total surface area exposed to the surroundings =
Surface area of the ball - $150 \times \pi {r^2} + 150 \times 2\pi {r^2}$ .
$
= 16.81\pi + 150\pi {r^2} \\
= \left\{ {16.81\pi + 150 \times \pi \times {{\left( {\dfrac{2}{{10}}} \right)}^2}} \right\}c{m^2} \\
= (16.81\pi + 6\pi )c{m^2} \\
= 22.81\pi c{m^2} \\
$
Here we will take $\pi = \dfrac{{22}}{7}$.
Therefore, total surface area exposed to the surrounding = $\left( {22.81 \times \dfrac{{22}}{7}} \right)c{m^2} = 71.68c{m^2}$
This is the required answer.
Note: In this type of question, first we have to know what is given and what we have to find in the question. Here we were asked the total surface area of a golf ball which is exposed to the surroundings . Here, we have found the total surface area of the ball and then we have removed the area occupied by the 150 dimplets each of given radius . we have removed only the $\pi {r^2}$ area of the dimplet as shown in the figure. Through this we got the answer.
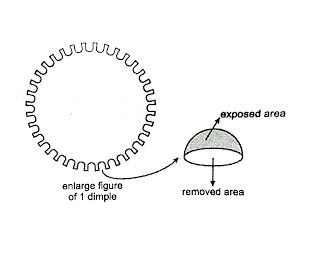
Surface area of a sphere = $4\pi {r^2}$. And then we will remove the area of each dimplet from the total surface area.
Complete step-by-step answer:
Given that, diameter of golf ball = $4.1cm$
$ \Rightarrow {\text{ radius of the ball = }}\dfrac{{diameter}}{2} = \dfrac{{4.1}}{2}cm$
Radius of each dimplet = $2mm = \dfrac{2}{{10}}cm$.
We have,
$ \Rightarrow $ Surface area of the golf ball = $4\pi {r^2}$
$ \Rightarrow $ Surface area of the golf ball = $4 \times \pi \times {\left( {\dfrac{{4.1}}{2}} \right)^2} = 16.81\pi c{m^2}$ .
Here, there are a total of 150 dimplets present on the surface of the golf ball. Each dimplet occupies some area.
In case of each dimple, surface area is equals to $\pi {r^2}$ ( where r is the radius of each dimple ) is removed from the total surface area of the golf ball where as the surface area of the hemisphere i.e. $2\pi {r^2}$ is exposed from the surroundings.
So, total surface area exposed to the surroundings =
Surface area of the ball - $150 \times \pi {r^2} + 150 \times 2\pi {r^2}$ .
$
= 16.81\pi + 150\pi {r^2} \\
= \left\{ {16.81\pi + 150 \times \pi \times {{\left( {\dfrac{2}{{10}}} \right)}^2}} \right\}c{m^2} \\
= (16.81\pi + 6\pi )c{m^2} \\
= 22.81\pi c{m^2} \\
$
Here we will take $\pi = \dfrac{{22}}{7}$.
Therefore, total surface area exposed to the surrounding = $\left( {22.81 \times \dfrac{{22}}{7}} \right)c{m^2} = 71.68c{m^2}$
This is the required answer.
Note: In this type of question, first we have to know what is given and what we have to find in the question. Here we were asked the total surface area of a golf ball which is exposed to the surroundings . Here, we have found the total surface area of the ball and then we have removed the area occupied by the 150 dimplets each of given radius . we have removed only the $\pi {r^2}$ area of the dimplet as shown in the figure. Through this we got the answer.

Recently Updated Pages
A man running at a speed 5 ms is viewed in the side class 12 physics CBSE

State and explain Hardy Weinbergs Principle class 12 biology CBSE

Which of the following statements is wrong a Amnion class 12 biology CBSE

Two Planoconcave lenses 1 and 2 of glass of refractive class 12 physics CBSE

The compound 2 methyl 2 butene on reaction with NaIO4 class 12 chemistry CBSE

Bacterial cell wall is made up of A Cellulose B Hemicellulose class 12 biology CBSE

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

State the principle of an ac generator and explain class 12 physics CBSE

Sketch the electric field lines in case of an electric class 12 physics CBSE

Give 10 examples of unisexual and bisexual flowers




