Question

A glass full of water has a bottom of area \[20c{m^2}\], top of area \[20c{m^2}\], height 20 cm and volume half a litre. (i) Find the force exerted by the water on the bottom (ii) considering the equilibrium of water, find the resultant forces exerted by the sides of the glass on the water.

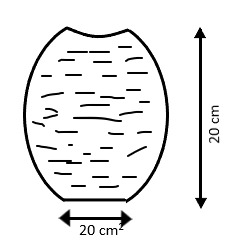
[\[{\text{atmospheric pressure = 1}}{\text{.0}} \times {\text{1}}{{\text{0}}^5}{\text{ N}}{{\text{m}}^{ - 2}},{\text{ Density of water = 1000 kg}}{{\text{m}}^{ - 3}}{\text{ and g = 10 m}}{{\text{s}}^{ - 2}}\]]
(i) 104 N (ii) 5 N downward
(i) 304 N (ii) 10 N downward
(i) 204 N (iii) 1 N upward
(i) 404 N (iii) 5 N upward

Answer 1

Hint : The pressure in a vessel filled by a fluid is independent of the shape of the fluid. Some of the weight of the water will be balanced by the sides of the glass at the bottom.

Formula used: In this solution we will be using the following formula;
\[F = PA\] where \[F\] is the force exerted on a surface, \[P\] is the pressure exerted on the same surface, and \[A\] is the total area of the surface.
\[P = {P_{atm}} + \rho gh\] where \[{P_{atm}}\] is the atmospheric pressure at the particular location, \[\rho \] is the density of the fluid, \[g\] is the acceleration due to gravity, and \[h\] is the depth of location of interest from the free surface of the liquid.

Complete step by step answer
It is generally known that any liquid in a containing vessel exert a pressure of that vessel due to the weight of the liquid and the atmospheric pressure exerted on the liquid. The pressure is independent of the shape of the body and dependent on the depth from the free surface. It is given as
\[P = {P_{atm}} + \rho gh\] where \[{P_{atm}}\] is the atmospheric pressure at the particular location, \[\rho \] is the density of the fluid, \[g\] is the acceleration due to gravity, and \[h\] is the depth of location of interest from the free surface of the liquid.
Hence, the substituting all known values from our question, we have
\[P = 1 \times {10^5} + 1000 \times 10 \times \left( {20 \times {{10}^{ - 2}}} \right)\] (since \[1cm = {10^{ - 2}}m\])
Hence, by computation, we have
\[P = 10000 + 2000 = 102000{\text{ N/}}{{\text{m}}^2}\]
Therefore, for the force exerted by the surface we recall that
\[F = PA\] where \[F\] is the force exerted on a surface, \[P\] is the pressure exerted on the same surface, and \[A\] is the total area of the surface.
Thus, by insertion of known values, we get
\[F = 102000 \times \left( {20 \times {{10}^{ - 4}}} \right)\] (since \[1c{m^2} = {10^{ - 4}}{m^2}\])
Hence,
\[F = 204{\text{ N}}\]
To calculate the resultant of the side glass on the water, we recall that for equilibrium, upward forces must balance downward forces hence, the weight of the liquid must balance the vertical component of the force the glass exerts on the water. The vertical force of the glass on the water is the sum of the pressure force on the flat bottom plus the vertical component of the forces due to the sides. Hence,
\[W = {P_{flat}}A + {F_s}\] where \[W\] is the weight, \[{P_{flat}}A\] is the net force exerted on the water by the flat surface, and \[{F_s}\] is the net force exerted by the sides on the water in the vertical direction.
The weight of the water is given by
\[W = \rho Vg\]
\[ \Rightarrow W = 1000 \times \left( {0.5 \times {{10}^{ - 3}}} \right) \times 10\] (since \[1litre = {10^{ - 3}}{m^3}\])
By computation, we get
\[W = 5N\].
The net force exacted by the bottom flat glass on the water is given as
\[{P_{flat}}A = \rho ghA\] hence,
\[{P_{flat}}A = 1000 \times 10 \times 0.2 \times 0.002 = 4N\].
Hence, the force by the side glasses is calculated as
\[{F_s} = W - {P_{flat}}A = 5 - 4\]
\[ \Rightarrow {F_s} = 1N\]
Since, the weight acts downward, the vertical force which balances it must act upwards.
Hence, \[{F_s} = 1N\], upwards.
Thus, the correct option is C

Note
We should take note that for examination purposes, alternatively, we can conclude that option C is the answer without calculating for the resultant force by sides of the glass on the water since the only option with \[204{\text{ N}}\] is option C.
Also, the force exerted by the glass on the water has no atmospheric pressure because we considered only the part of the force which balances the weight of the water. Nevertheless, it could be added that atmospheric pressure acts on both sides (up and down) hence cancels out of the expression.