Question

A glass capillary tube of internal radius $r=0.25mm$ is immersed in water. The top end of the tube is projected by $2cm$ above the surface of the water. At what angle does the liquid meet the tube? Surface tension of water $=0.07N/m$.
$A)\text{ }\theta ={{90}^{0}}$
$B)\text{ }\theta ={{70}^{0}}$
$C)\text{ }\theta ={{45}^{0}}$
$D)\text{ }\theta ={{35}^{0}}$

Answer 1

Hint: This problem can be solved by using the formula for the capillary rise of a liquid in a capillary tube when the tube is immersed in the liquid. First we have to check whether the capillary rise of water in the tube will be more than the height of the tube or not. If yes, then the contact angle will change accordingly so as to accommodate the same height of the liquid by changing the contact angle.

Formula used:
$h=\dfrac{2T\cos \theta }{r\rho g}$

Complete answer:
When a capillary tube of enough height is given, then the contact angle of water with glass is zero. However, if the height of the capillary tube for the capillary rise is not enough, then the water will curve at the top of the capillary, so as to accommodate the total height and volume of the water. Hence, the contact angle will change.
The capillary rise $h$ of a liquid of density $\rho $ and surface tension $T$ in a capillary tube of internal radius $r$ is given by
$h=\dfrac{2T\cos \theta }{r\rho g}$ ---(1)

Where $\theta $ is the angle of contact made by the liquid with the surface of the tube and $g$ is the acceleration due to gravity.
Hence, let us first find out the capillary height rise of the water in the given glass capillary tube.

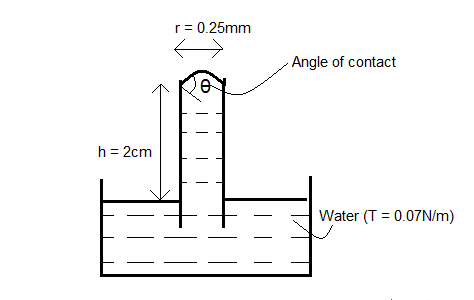
The given internal radius of the tube is $r=0.25mm=0.25\times {{10}^{-3}}m$ $\left( \because 1mm={{10}^{-3}}m \right)$.

The density of water is $\rho ={{10}^{3}}kg/{{m}^{3}}$.
The given surface tension of water is $T=0.07N/m$.
The acceleration due to gravity is $g=9.8m/{{s}^{2}}$.
Let the capillary rise in this case be ${{h}_{0}}$.
The angle of contact of glass with water is ${{\theta }_{0}}={{0}^{0}}$.
Hence, using (1), we get,
${{h}_{0}}=\dfrac{2T\cos {{0}^{0}}}{r\rho g}=\dfrac{2\times 0.07\times \cos {{0}^{0}}}{0.25\times {{10}^{-3}}\times {{10}^{3}}\times 9.8}=\dfrac{0.14\times 1}{2.45}=0.057m=5.7cm$ --(2) $\left( \because \cos {{0}^{0}}=1,\text{ }1m=100cm \right)$

Hence, as we can see, the capillary rise is more than the height of the given capillary tube above the surface of the water, that is, $2cm$.
Hence, the upper surface of the liquid will curve, so as to accumulate the same volume of water as of the original capillary rise, that is, $5.7cm$.
Hence, now let the angle of contact be $\theta $ and the capillary rise will be $h=2cm$.
Hence, using (1), we get,

$h=\dfrac{2T\cos \theta }{r\rho g}$
Using (2), we get,
$h={{h}_{0}}\cos \theta $
$\therefore \cos \theta =\dfrac{h}{{{h}_{0}}}=\dfrac{2}{5.7}$
$\therefore \theta ={{\cos }^{-1}}\left( \dfrac{2}{5.7} \right)={{\cos }^{-1}}\left( 0.35 \right)={{69.5}^{0}}\approx {{70}^{0}}$
Hence, the required angle of contact is ${{70}^{0}}$.
Therefore, the correct option is $\text{ }\theta ={{70}^{0}}$.

So, the correct answer is “Option B”.

Note:
Students might sometimes directly go on to calculate the angle of contact by considering that the capillary rise will be more than the projection of the capillary tube above the surface of the liquid. However, this is not always true and students must not jump to this conclusion. Students should always check first whether the capillary rise will be more than the height of the tube actually and only then the contact angle will change. Sometimes questions are set purposefully in this way to check whether students perform this preliminary step or not. If not, they may arrive at the wrong answer.