Question

A girl whose eyes are 150 cm above the ground looks at her reflection in a vertical mirror 250 cm away. The top and bottom of the mirror are 200cm and 120cm above the ground respectively. What length below her eyes can she see of herself in the mirror?
A. 60cm
B. 75cm
C. 100cm
D. 120cm

Answer 1

Hint: To solve the given question, understand what values are given and construct a ray diagram. Then use the law of reflection, which says that the angle of incidence and the angle of reflection are always equal and find the length of the image that the girl can see below her eye level.

Complete step by step answer:
It is given that a girl is standing in front of a plane vertical mirror. It is said that the eyes of the girl are 150 cm above the ground level and look into the mirror. And the tip of the mirror is said to be at a height of 200 cm above the ground level and the bottom of the mirror is at a height of 120 cm.

Now, the length of the image of herself, which the girl can see, depends on the field of light that is coming back to her after reflecting at the plane mirror.

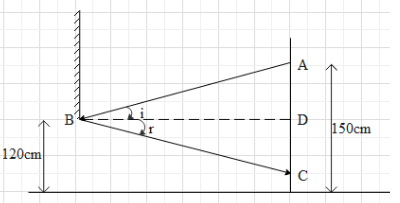
From the above figure and by using the law of reflection, we get that the angles i and r are equal. We can understand that $\Delta ABD\cong \Delta CBD$ by ASA congruence rule.
Then by CPCT we get that AD = CD.
However, we know that $AD=AP-DP$
And $AP=150cm,DP=120cm$.
This means that $AD=150-120=30cm$
This further means that $AD=CD=30cm$
From the figure, we get that the length of the image of herself (below her eye level) that the girl can see is equal to $l=AD+CD$
$\therefore l=30+30=60cm$

Hence, the correct option is A.

Note: Note that the length of the image of the girl, that the girl can see inside the mirror does not depend on the distance between the mirror and the girl. In this case, the girl will always see a length of 60 cm of herself (below her eye level) at every position, in front of the mirror.