Question

A girl of height 90 cm is walking away from the base of a lamp post at a speed of 1.2 m/s. If the lamp is 3.6 m above the ground, find the length of her shadow after 4 seconds.

Answer 1

Hint: First of all, draw the diagram of the given data, it will give us an idea of what we have to find. Then find the distance travelled by the girl by using distance-speed formula. And show that the formed triangles in the diagram are congruent and hence find the shadow of the girl.

Complete step-by-step answer:
Given length of lamp post AB = 3.6 m
Height of the girl CD \[ = 90{\text{ cm}} = \dfrac{{90}}{{100}}{\text{ m}} = 0.9{\text{ m}}\]
Speed = 1.2 m/sec
Here we have to find the length of the girl’s shadow i.e., DE as shown in the below figure:

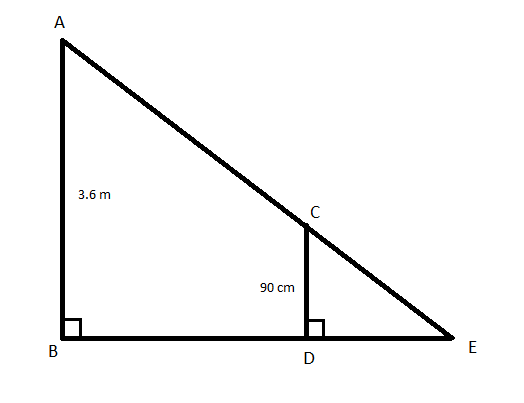
The girl walks BD distance in 4 seconds.
We know that
\[\
  {\text{Speed}} = \dfrac{{{\text{Distance}}}}{{{\text{Time}}}} \\
  1.2 = \dfrac{{BD}}{4} \\
  BD = 1.2 \times 4 = 4.8{\text{ m}} \\
\]
Now, in \[\Delta ABE\] and \[\Delta CDE\]
\[
   \Rightarrow \angle E = \angle E{\text{ }}\left( {{\text{common}}} \right) \\
   \Rightarrow \angle B = \angle D{\text{ }}\left( {{\text{Both 9}}{{\text{0}}^0}{\text{ because lamp post as well as the girl are standing vertical to the ground}}} \right) \\
\]
Therefore, using AA criterion we have \[\Delta ABE \cong \Delta CDE\]
We know that if two triangles are similar, then their sides are in proportion
\[
  \dfrac{{BE}}{{DE}} = \dfrac{{AB}}{{CD}} \\
  \dfrac{{BD + DE}}{{DE}} = \dfrac{{AB}}{{CD}} \\
  \dfrac{{4.8 + DE}}{{DE}} = \dfrac{{3.6}}{{0.9}} \\
  4.8 + DE = 4DE \\
  4DE - 3DE = 4.8 \\
  DE = \dfrac{{4.8}}{3} \\
  \therefore DE = 1.6{\text{ m}} \\
\]
Hence the length of the girl’s shadow after 4 seconds is 1.6 m.

Note: If two triangles are similar, then their sides are in proportion. The AA similarity criterion tells us that two triangles are similar if two corresponding angles are equal to each other. Here we have converted cm into m by using the conversion 1 m = 100 cm.