Question

A galvanometer has resistance of 30 ohm and current of 2mA is needed to give a full-scale deflection. What is the resistance needed and how is it to be connected to convert the galvanometer:
a. into an ammeter with a range of 0.3 ampere
b. into a voltmeter with a range of 0.2 volt

Answer 1

Hint:Galvanometer is a device which can only be used to detect the presence of current. This device cannot be used directly, to measure the magnitude of the current and voltage in the circuit. Hence, we have to make some additions to the circuit to convert a galvanometer to serve our purpose whether we need it to calculate the magnitude of current or the voltage.

Complete step-by-step answer:
The galvanometer is a device which is used to detect the presence of current in a circuit and which displays the direction of flow of current.
An ammeter is a device used to measure the current in a branch of the circuit. It is always connected in series with the branch that you want to measure the current.
A voltmeter is a device used to measure the voltage across a circuit. It is connected in parallel to the branch that you want to measure the potential difference.
Both of these instruments can be constructed by making simple additions to a galvanometer.
i) Ammeter
To convert a galvanometer into an ammeter, an exceedingly low resistance called shunt is connected parallel to the galvanometer as shown:

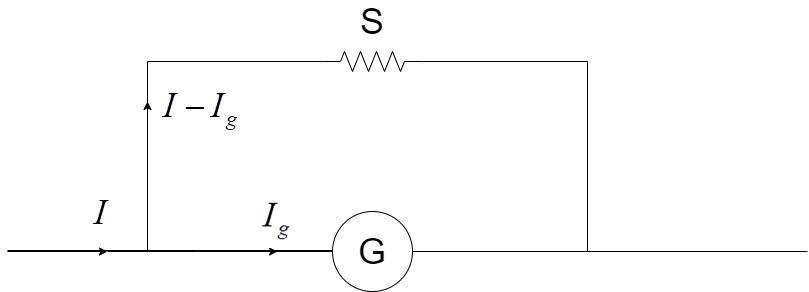
Here the resistance of the galvanometer is denoted by G.
The current in the circuit to be measured or the full range value (maximum range to be measured by the galvanometer) is $I$.
${{I}_{g}}$ is the current required for the full-scale deflection of the galvanometer.
The shunt resistance connected across the galvanometer, S, is calculated by the formula:
$S=\dfrac{G{{I}_{g}}}{I-{{I}_{g}}}$
Given in the question:
Range of the ammeter, $I=0\cdot 3A$
Full scale deflection current for the galvanometer, ${{I}_{g}}=2mA=0\cdot 002A$ Resistance of the galvanometer, $G=30\Omega $
The shunt resistance,
$S=\dfrac{30\times 0\cdot 002}{0\cdot 3-0\cdot 002}=\dfrac{0\cdot 06}{0\cdot 298}=0\cdot 201\Omega $
So, you can convert the galvanometer into an ammeter of range 0.3A by connecting a shunt resistor of $S=0\cdot 201\Omega $ parallel to the galvanometer.

ii) Voltmeter
To convert a galvanometer into a voltmeter, an exceedingly high series resistance is connected in series with the galvanometer as shown:

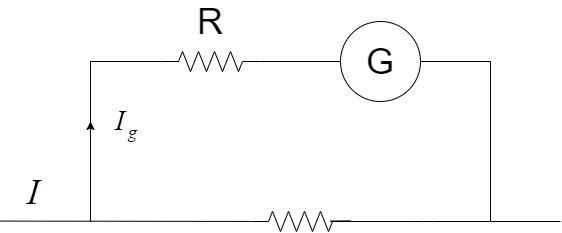
Here the resistance of the galvanometer is G and the current ${{I}_{g}}$ branches out from the main branch to flow into the voltmeter i.e. the series combination.
The series resistance connected to the galvanometer is given by –
$R=\dfrac{V}{{{I}_{g}}}-G$
Given in the question:
Range of the voltmeter, $V=0\cdot 2A$
Full scale deflection current for the galvanometer, ${{I}_{g}}=2mA=0\cdot 002A$
Resistance of the galvanometer, $G=30\Omega $
The series resistance,
$R=\dfrac{0\cdot 2}{0\cdot 002}-30=100-30=70\Omega $
To convert the galvanometer into a voltmeter, a high resistor of resistance $R=70\Omega $ should be connected in series with the galvanometer.

Note: The value of shunt resistance will be a very low value, usually less than 1 and the value of the series resistance will always be a very high number, usually, in 100s of ohms. So, when you are solving a question on conversion of a galvanometer, always keep this fact in mind so that you are sure that you are on the right track and that you do not make any mistakes such as getting a very high value of shunt resistance.