Question

A fish in a lake is at a \[6.3{\text{ }}m\] distance from the edge of the lake. If It is just able to see a tree on the edge of the lake, Its depth in the lake is ____ m. Refractive index of the water is 1.33.
A. \[6.30\]
B. \[5.52\]
C. \[7.5\]
D. \[1.55\]

Answer 1

Hint: To solve this problem, i.e., to find the depth of the lake, we will first draw a rough figure of using all the given information. Then we will again draw a figure of a right-angled triangle. Then after putting the values in the formula of critical angle we will get our required answer.

Complete step by step answer:
We have been given that a fish in a lake is at a distance of \[6.3{\text{ }}m\] from the edge of the lake. It is given that the fish is just able to see a tree on the edge of the lake. We need to find the depth of fish in the lake.Let us draw a figure using the given information, to understand better.

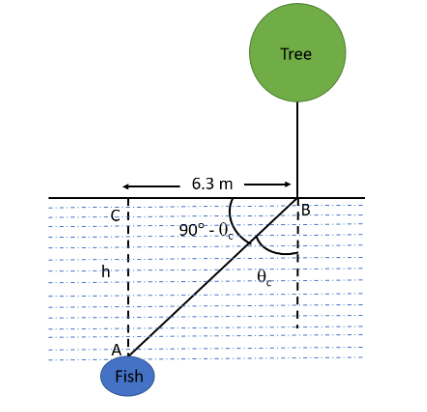
Here, in the diagram, ${\theta _c} = $ critical angle.
We know that, $Sin{\theta _c} = \dfrac{1}{\mu }$\[ \ldots \ldots eq.\left( 1 \right)\]
It is given that the refractive index of the water is 1.33. So, on putting the value in the above equation, we get
$
\Rightarrow Sin{\theta _c} = \dfrac{1}{{1.33}} \\
\Rightarrow Sin{\theta _c} = \dfrac{1}{{4/3}} = \dfrac{3}{4}........eq.(2) \\
$

From the $\Delta $ABC, we get
$\Rightarrow \tan (90 - {\theta _c}) = \dfrac{h}{{6.3}} \\
\Rightarrow \cot {\theta _c} = \dfrac{h}{{6.3}}...........[\because \tan (90 - x) = \cot x] \\
\Rightarrow h = (6.3)\cot {\theta _c} \\
$
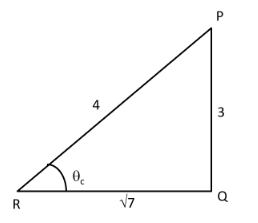
 Now, from the $\Delta $PQR, we get
$
\Rightarrow h = (6.3)\dfrac{{\sqrt 7 }}{3}............[\because \cot x =
\dfrac{{base}}{{perpendicular}}] \\
\Rightarrow h = (6.3)\dfrac{{2.64}}{3}...........[\because \sqrt 7 = 2.64] \\
\Rightarrow h = 5.52m \\
$
So, the depth in the lake is 5.52 m.
Thus, option (B) \[5.52\], is correct.

Note: To solve this question, it would be better if students draw the diagram properly, as it will give you a better idea. And in the solution, the relation which we have used is a relationship between critical angle and refractive index. Critical angle is inversely proportional to the refractive index.