Question

A film of water is formed between two straight parallel wires each $10\; cm$ long and at a separation of $0.5\;cm$. Calculate the work required to increase the distance between them by $1\;mm$. (Surface tension of water = $72 \times 10^{-3}\;Nm^{-1}$)

Answer 1

Hint: A good starting point would be to determine the change in the area of the film caused by the increase in distance. Once you have obtained this think of how you could relate that to the surface tension and work done. In other words, we know that surface energy is the work done per unit area in accommodating the extra area that is created. Use this as an analogy to surface tension following which, arriving at the result would be pretty straightforward.

Formula Used: The work done by the film when their area is increased:
$W = S \times \Delta A $ where S is the surface tension and $\Delta A$ is the consequent change in the area.

Complete step-by-step solution:

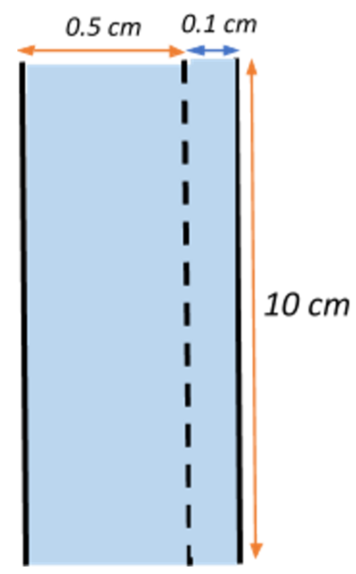
Let us begin by first listing out what is given to us.
We have the length of the wires, $l = 10\;cm = 0.1\;m$ each.
The two wires are arranged parallel to each other throughout.
We are given with the initial width of separation between the two wires, $w = 0.5\;cm = 5 \times 10^{-3}\;m$
The change in the width of separation is $\Delta w = 1\;mm = 1 \times 10^{-3\;m}$
The change in width causes a change in the area of the separation between the two wires, i.e.,
Change in area $\Delta A =l \times \Delta w = 0.1 \times 10^{-3} = 10^{-4}\;m^{2} $
Now, let us understand what surface tension means.
Surface tension can be thought of as a physical force acting on the surface of a liquid that results in a molecule pulling in its neighboring molecules from all directions, arising from the cohesive nature of liquid molecules.
The molecules in the film of water between the two parallel wires also experience these cohesive forces that hold the film together. Therefore, when we increase the distance between the two wires, the surface tension acts as a force and contributes to the work done in accommodating this increase in the area while at the same time maintaining the integrity of the film from all the way down to the molecular level. Hence, the surface tension of water acts in resistance to external forces by maintaining the cohesiveness between the water molecules. Surface energy, however, accounts for the disrupted intermolecular bonds when a surface or film is created. This is basically the work done per unit area by the surface-creating force (which is nothing but the surface tension).
Quantitatively, the work done by the film when the distance between the two wires is increased can be given as:
$W = S \times \Delta A $
Accounting for the contact that the water film has with the surface of both the wires, we thus get:
$W = (72 \times 10^{-3}) \times (2 \times 10^{-4}) = 144 \times 10^{-7}\; joules$

Note: Remember that a molecule in bulk liquid experiences cohesive forces with other molecules in all directions whereas a molecule at the surface of the liquid, or a thin film, experiences only net inward cohesive forces.
Surface tension on a liquid surface makes the surface behave like as if it were a stretched elastic membrane:
Small insects such as grasshoppers can walk on water because the surface tension at the surface of the water does not allow its weight to push through.
 Also, droplets of water tend to be pulled into a spherical shape by the cohesive forces on the surface layer to minimize the wall tension of the surface layer. This is also the same reason why bubbles are round in shape.