Question

A father is 30 years older than his son. In 12 years, the man will be three times as old as his son. Find their present ages.

Answer 1

Hint: Assume the present age of the son is x, and that of the father is y. Use the statement of the question to form two linear equations in two variables x and y. Solve the system of equations using substitution or elimination method or graphically or using matrices. Hence find the value of x and y. The value of x will be the present age of the son, and the value of y will be the present age of the father.



Complete step-by-step answer:
Let the present age of the son be x, and that of the father be y.
Since the father is 30 years older than his son, we have
y =x+30 (i).
Also, after 12 years, the father's age will be three times that of his son. So, we have
y+13 = 3(x+13)
expanding the term on RHS, we get
y+13 = 3x+39
Subtracting 13 from both sides, we get
y+13 -13= 3x+39-13
i.e. y = 3x+26 (ii)
Substituting the value of y from equation (i) in equation (ii), we get
x+30=3x+26
Subtracting x from both sides, we get
x+30-x=3x+26-x
i.e. 30=2x+26
Subtracting 20 from both sides, we get
30-26 = 2x+26-26
i.e. 2x = 4
Dividing both sides by 2, we get
$\begin{align}
  & \dfrac{2x}{2}=\dfrac{4}{2} \\
 & \Rightarrow x=2 \\
\end{align}$
Hence x = 2.
Substituting the value of x in equation (ii), we get
y = 2+30=32.
Hence the present age of the son is 2 years, and the present age of his father is 32 years.

Note: Alternatively, we can plot the system of equations on a graph. The point where these lines intersect is the solution of the given system.
The graph of the above system is shown below

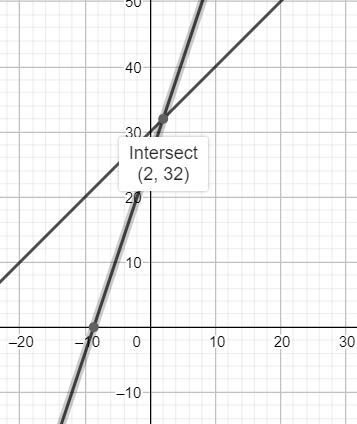
As is evident from the graph, the lines intersect at (2,32).
Hence x =2 and y =32, which is the same as obtained above.