Question

A farmer $ {{F}_{1}} $ has a land in the shape of a triangle with vertices at $ P\left( 0,0 \right), Q\left( 1,1 \right) $ and $ R\left( 2,0 \right) $ . From this land, a neighbouring farmer $ {{F}_{2}} $ takes away the region which lies between the side PQ and a curve of the form $ y={{x}^{n}}\left( x>1 \right) $ . If the area of the region taken away by the farmer $ {{F}_{2}} $ is exactly 30% of the area of $ \Delta PQR $ , then the value of n is _________?

Answer 1

Hint: since the land possessed by farmer $ {{F}_{1}} $ is in the form of a triangle, we find the area of the triangle first. Then we draw a triangle and give a curve $ y={{x}^{n}}\left( x>1 \right) $ . We find the equation of side PQ and find the area lies between side PQ and $ y={{x}^{n}}\left( x>1 \right) $ by using the area under the curve by integration. Now, we use the given relation between two areas to find the value of n.

Complete step-by-step answer:
According to the problem, we can see that farmer $ {{F}_{1}} $ has land in the shape of a triangle.
We can see that coordinates of vertices of the triangle are $ P\left( 0,0 \right), Q\left( 1,1 \right) $ and $ R\left( 2,0 \right) $ .
Let us find the area of the triangle first for proceeding further in problem.
We know that area(A) of the triangle with the vertices \[({{a}_{1}},{{b}_{1}}),\left( {{a}_{2}},{{b}_{2}} \right)\] and $ \left( {{a}_{3}},{{b}_{3}} \right) $ is:
 $ A=\dfrac{1}{2}\times \left| \begin{matrix}
   {{a}_{1}}-{{a}_{2}} & {{a}_{1}}-{{a}_{3}} \\
   {{b}_{1}}-{{b}_{2}} & {{b}_{1}}-{{b}_{3}} \\
\end{matrix} \right| $ Sq.units, here $ \left| . \right| $ is determinant of $ 2\times 2 $ matrix.
We know that determinant of $ 2\times 2 $ matrix is:
 $ \left| \begin{matrix}
   p & q \\
   r & s \\
\end{matrix} \right|=\left( p\times s \right)-\left( q\times r \right) $
Using these formulae we find the area of the triangle PQR. Let it be $ {{A}_{1}} $ .
 $ {{A}_{1}}=\dfrac{1}{2}\times \left| \begin{matrix}
   0-1 & 0-2 \\
   0-1 & 0-0 \\
\end{matrix} \right| $
\[{{A}_{1}}=\dfrac{1}{2}\times \left| \begin{matrix}
   -1 & -2 \\
   -1 & 0 \\
\end{matrix} \right|\]
 $ {{A}_{1}}=\dfrac{1}{2}\times \left| \left( \left( -1\times 0 \right)-\left( -1\times -2 \right) \right) \right| $
 $ {{A}_{1}}=\dfrac{1}{2}\times \left| 0-\left( 2 \right) \right| $
 $ {{A}_{1}}=\dfrac{1}{2}\times \left| -2 \right| $
 $ {{A}_{1}}=\dfrac{1}{2}\times 2 $
 $ {{A}_{1}}=1sq.units......(1) $
We found an area of land that farmer $ {{F}_{1}} $ owns as 1sq.units.
According to the problem, it is given that farmer $ {{F}_{2}} $ takes some region of the land from farmer $ {{F}_{1}} $ in the form of $ y={{x}^{n}}\left( x>1 \right) $ which lies near the side PQ.
It is also said that the area of the region taken by the farmer $ {{F}_{2}} $ is equal to the 30% of the total area of the land PQR.
To find the value of ‘n’ using this information, we plot triangle PQR and curve $ y={{x}^{n}}\left( x>1 \right) $ on a graph.

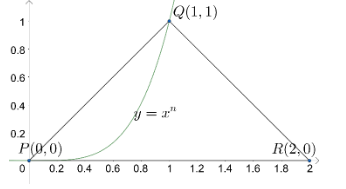
Let us find the equation of the side PQ.
We know that the equation of the line which is passing through \[\left( {{x}_{1}},{{y}_{1}} \right)\] and $ \left( {{x}_{2}},{{y}_{2}} \right) $ is $ y-{{y}_{1}}=\left( \dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}} \right)\times \left( x-{{x}_{1}} \right) $
Here we have points $ P\left( 0,0 \right) $ and $ Q\left( 1,1 \right) $ .
Now, the equation of side PQ is $ y-0=\left( \dfrac{1-0}{1-0} \right)\times \left( x-0 \right) $
 $ y=\dfrac{1}{1}\times x $
 $ y=x $
Now we find the area which lies between the side PQ and the curve $ y={{x}^{n}}\left( x>1 \right) $ .
We know that from area under curve by integration is defined as:
 $ \text{Area between two curves between x=a and x=b}=\int\limits_{a}^{b}{\left( equation of above curve-equation of below curve \right)dx} $
Let us assume the area between side PQ and curve $ y={{x}^{n}}\left( x>1 \right) $ be $ {{A}_{2}} $ .
Since the curve $ y={{x}^{n}}\left( x>1 \right) $ cuts the triangle between x=0 and x=1, we take those as limits for the integration. Here we can observe that side PQ lies above the curve $ y={{x}^{n}}\left( x>1 \right) $ .
 $ {{A}_{2}}=\int\limits_{0}^{1}{(x-{{x}^{n}})dx} $
We know that $ \int{{{x}^{k}}dx=\dfrac{{{x}^{k+1}}}{k+1}+C} $
 $ {{A}_{2}}=\left[ \dfrac{{{x}^{2}}}{2} \right]_{x=0}^{x=1}-\left[ \dfrac{{{x}^{n+1}}}{n+1} \right]_{x=0}^{x=1} $
We know for a definite integral $ \int\limits_{a}^{b}{f'(x)dx=f(b)-f(a)} $ .
 $ {{A}_{2}}=\left( \dfrac{{{1}^{2}}}{2}-\dfrac{{{0}^{2}}}{2} \right)-\left( \dfrac{{{1}^{n+1}}}{n+1}-\dfrac{{{0}^{n+1}}}{n+1} \right) $
 $ {{A}_{2}}=\left( \dfrac{1}{2}-\dfrac{0}{2} \right)-\left( \dfrac{1}{n+1}-\dfrac{0}{n+1} \right) $
 $ {{A}_{2}}=\left( \dfrac{1}{2}-0 \right)-\left( \dfrac{1}{n+1}-0 \right) $
 $ {{A}_{2}}=\dfrac{1}{2}-\dfrac{1}{n+1}......(2) $
We know that $ {{A}_{2}} $ is 30% of $ {{A}_{1}} $ .
So, we got $ \dfrac{1}{2}-\dfrac{1}{n+1}=0.3\times \left( 1 \right) $
 $ 0.5-\dfrac{1}{n+1}=0.3 $
 $ 0.5-0.3=\dfrac{1}{n+1} $
 $ 0.2=\dfrac{1}{n+1} $
 $ n+1=\dfrac{1}{0.2} $ \
 $ n+1=5 $
 $ n=4 $
∴ The value of n is 4.

Note: Area of the triangle can also be calculated by using $ \dfrac{1}{2}\times base\times height $ . Since a given triangle is an Isosceles triangle with equal sides PQ and QR, height can be calculated by finding the distance between Q and midpoint of side PR. Here we should not consider the area of the triangle as a negative value while calculating through the determinant as it cannot be a negative value.