Question

A disc of mass 1.0kg is kept floating horizontally in air by firing bullets of mass 0.05kg each vertically at it, at the rate of 10 per second. If the bullets rebound with the same speed, the speed with which these are fired will be

\[\begin{align}
  & \text{A}\text{. }0.098m/s \\
 & \text{B}\text{. 0}\text{.98m/s} \\
 & \text{C}\text{. 9}\text{.8m/s} \\
 & \text{D}\text{. 98}\text{.0m/s} \\
\end{align}\]

Answer 1

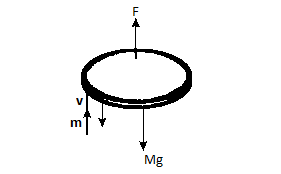
Hint: Here the disc is floating in air by firing bullets that means the disc is having the downward gravitational pull and a force due to change in momentum of the bullets as shown in the diagram. To get the speed of bullets we can balance the force experienced by the disc. Bullets rebound means they reflect back with the same speed.

Formula used:
\[F=m\dfrac{dv}{dt}\]

Complete answer:
From the given figure, we can see that there is an upward force due to the firing of bullets that is a change in momentum of the bullet. The velocity of the bullet is v and the rebounding velocity will be –v. There is also downward force gravitational force shown as Mg.
Now the upward force can be given by the Newton’s second law
\[F=m\dfrac{dv}{dt}\]
Where m is the mass of the bullet and change in velocity is given as
\[dv={{v}_{1}}-{{v}_{2}}\]
\[{{v}_{1}}\] is the velocity with which the bullet is fired and \[{{v}_{2}}\] is the rebounding velocity. As per question
\[{{v}_{1}}=v\text{ and }{{v}_{2}}=-v\]
Substituting values we get
 \[\begin{align}
  & dv=v-(-v) \\
 & dv=v+v=2v \\
\end{align}\]
And \[dt=1\]as we change is calculated for per second.
The downward gravitational pull is given as
\[F=Mg\]
Where M is the mass of the disc and g is acceleration due to gravity.
Now balancing the forces we get
\[Mg=m\dfrac{dv}{dt}\]
Where \[M=1kg,g=9.8m/s,m=0.05kg\times 10,dt=1,dv=2v\]
Mass of the bullet is multiplied with ten as ten bullets are fired per second.
Substituting above values in the equation we get
\[1\times 9.8=0.05\times 10\times 2v\]
Solving for v we get
 \[\begin{align}
  & v=\dfrac{1\times 9.8}{0.05\times 10\times 2} \\
 & v=9.8m/s \\
\end{align}\]
Hence the velocity of the bullet is \[9.8m/s\].

So, the correct answer is “Option C”.

Note:
We have to multiply the mass of the bullet by the number of bullets fired per second on the disc as the disc is floating due to the total force exerted on it by each bullet. Value of g may vary, sometimes the value of g is given in the question and it can change the answer. Also, the units should be used properly, in case the mass of the bullet was given in grams then we have to change it in kilograms first and then use it.