Question

A disc is placed on a truck, which is accelerating with ‘a’. The disc is rolling. Find the relation between the acceleration of the truck and the angular acceleration of the disc. Mass of the disc is ‘m’ and radius ‘r’.

Answer 1

Hint: Let, the magnitude of instantaneous linear acceleration is \[\overrightarrow a \] and that of angular acceleration is $'\alpha '$ . Now calculate the value of acceleration of centre of mass of the disc by considering the acceleration of each small particle of the disc.

Complete step by step answer:
The magnitude of instantaneous linear acceleration is equal to the product of the magnitude of instantaneous angular acceleration and radius of any circular object.
So, let, the magnitude of instantaneous linear acceleration is \[\overrightarrow a \] and that of angular acceleration is $'\alpha '$ and it is given (in the question) that the radius of the disc is ‘r’.
So, $\overrightarrow a = \alpha \times r$

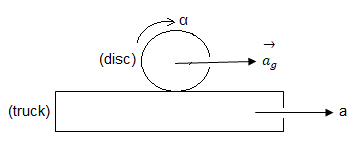
Now from the above picture,
‘a’ is the acceleration of the truck (given), $\overrightarrow {{a_g}} $ is the acceleration the rolling disc with respect to the ground (of the centre of mass), $\alpha $ is the angular acceleration of the centre of mass of the disc.
Now, if the tangential direction is through the mutual point between the truck and the disc, then only the condition of pure rolling is achieved.
So, the condition of pure rolling is,
$\overrightarrow {{a_g}} - \alpha r = a$ ………(1)
Now, the centre of mass of an extended body or a system of particles is such a unique point that, any force applied through that point produces only tangential motion. So, let us consider the acceleration of the each particle of the disc are ${a_1},{a_2},{a_3},.....{a_n}$ of the masses ${m_1},{m_2},{m_3},......,{m_n}$ respectively, and ‘m’ is the total mass of the disc.
So, the acceleration of the centre of mass will be,
$\overrightarrow {{a_g}} = \dfrac{{{m_1}{a_1} + {m_2}{a_2} + ...... + {m_n}{a_n}}}{{{m_1} + {m_2} + ......{m_n}}}$
$ \Rightarrow \overrightarrow {{a_g}} = \dfrac{{\sum\limits_{i = 1}^n {{m_i}{a_i}} }}{m}$
Therefore, the relation between the acceleration of the truck and the angular acceleration the disc is,
 $\dfrac{{\sum\limits_{i = 1}^n {{m_i}{a_i}} }}{m} - \alpha r = a$ {By putting the value of $\overrightarrow {{a_g}} $ in equation (1)}


Note: If the angular acceleration is positive, its direction is the same as that of angular velocity. But when the angular acceleration is negative, its direction is opposite to that of angular velocity. It should be remembered that in the case of pure rotation, linear acceleration changes its direction continuously, but the direction of angular acceleration remains unaltered. Whenever the axis of rotation remains fixed, the direction of angular acceleration does not change.