Question

A cylindrical tin with a diameter of base 20 cm and height 25 cm is open at the top. Find the cost of painting the tin at Rs. 300 per \[{{m}^{2}}\]. (Use \[\pi =3.14\])
(a) Rs. 56.57
(b) Rs. 56.51
(c) Rs. 55.52
(d) Rs. 56.50

Answer 1

Hint:First of all find the surface area of the cylindrical tin to be painted by subtracting the area of the top from the total surface area of the cylindrical tin. Now multiply it to the cost / \[{{m}^{2}}\] to get the total cost.

Complete step-by-step answer:
In this question, we are given a cylindrical tin with the diameter of base 20 cm and height 25 cm which is open on the top. We have to find the total cost of painting the tin at Rs. 300 per \[{{m}^{2}}\] (\[\pi =3.14\]).
Let us draw the diagram of the cylindrical tin to visualize the question.

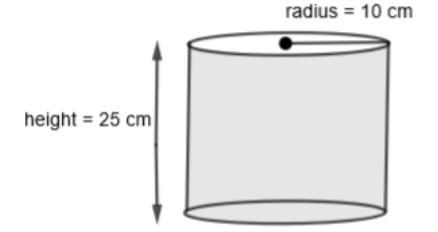
We know that the total surface area of the cylinder is \[2\pi r\left( r+h \right)\] where r and h are the radius and height of the cylinder respectively. So, we get the total surface area of the cylindrical tin as \[2\pi r\left( r+h \right)\]. But we are given that the cylindrical tin is open at the top, so we will subtract this area from the total surface area. So, we get,
The surface area of the given cylindrical tin \[=2\pi r\left( r+h \right)\]- (Area of the top)
We know that the top of the cylinder is made by the circle and the area of the circle is \[\pi {{r}^{2}}\]. So, we get the area of the top of the cylindrical tin as \[\pi {{r}^{2}}\]. Hence, we get,
The surface area of the given cylindrical tin \[=2\pi r\left( r+h \right)-\pi {{r}^{2}}\]
By substituting the value of \[r=\dfrac{20}{2}=10cm\] and h = 25 cm in the above equation, we get,
The surface area of the given cylindrical tin \[=\left[ 2\pi .10\left( 10+25 \right)-\pi {{\left( 10 \right)}^{2}} \right]\]
\[=\left[ 20\pi \left( 35 \right)-100\pi \right]c{{m}^{2}}\]
\[=\left[ 700\pi -100\pi \right]c{{m}^{2}}\]
\[=600\pi \text{ c}{{m}^{2}}\]
By substituting the value of \[\pi =3.14\] in the above equation, we get,
The surface area of the given cylindrical tank \[=600\times 3.14\text{ c}{{m}^{2}}=1884\text{ c}{{m}^{2}}\]
We know that \[1c{{m}^{2}}={{10}^{-4}}{{m}^{2}}\]
So, we can write the area as,
\[1884\times {{10}^{-4}}=0.1884{{m}^{2}}\]
Now, we are given that the cost of painting the tin is Rs. 300 /\[{{m}^{2}}\]. So, we get,
The total cost of painting the surface area of the cylindrical tin \[=\left( 0.1884{{m}^{2}} \right).\left( Rs.300/{{m}^{2}} \right)=Rs.56.51\]
Hence, we get the total cost of painting the cylindrical tin as Rs. 56.51.
Therefore the correct option is (b).

Note: In this question, some students make this mistake of taking the diameter as the radius of the given object. So this mistake must be avoided and diameter should be divided by two to get the radius and then only should be substituted in the given formula. Also, some students take the curved surface area in this question but the base area should be taken along with the curved surface area. So this should be taken care of.And also students should take care of the units while solving these types of problems.