Question

A cylindrical metallic rod in thermal contact with two reservoirs of heat at its two ends conducts an amount of heat \[Q\] in time \[t\]. The metallic rod is melted and the material is formed into a rod of half the radius of the original rod. What is the amount of heat conducted by the new rod, when placed in thermal contact with the two reservoirs in time $t$?
(A) $\dfrac{Q}{4}$
(B) $\dfrac{Q}{{16}}$
(C) \[2Q\]
(D) \[\dfrac{Q}{2}\]

Answer 1

Hint To solve this question, we need to use the formula for the heat conducted across a conductor per unit time. We need to assume the dimensions of the rod and the temperature of the reservoir. Putting these in the formula, we will get the expression for \[Q\]. Then applying the same formula for the second case, we will get the expression for the heat conducted in time $t$, which when compared with the previous expression will come in terms of \[Q\].

Formula used: The formula used to solve this question is given by
$\dfrac{q}{T} = k\dfrac{{A\Delta T}}{l}$, here $Q$ is the heat conducted in time $t$ across a conductor of length $l$, area of cross section $A$ and the material of thermal conductivity of $k$, and is subjected to the temperature difference of $\Delta T$ across its ends.

Complete step-by-step solution:
Let the length, the area of cross section, and the thermal conductivity of the metallic rod be $L$, ${A_1}$, and $K$ respectively. Also, let the temperature of the thermal reservoirs be ${T_1}$ and ${T_2}$. We can represent this situation in the below figure.

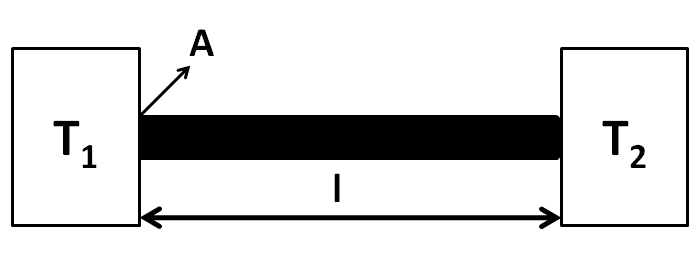
We know that the rate of heat conducted per unit time is given by
$\dfrac{q}{T} = k\dfrac{{A\Delta T}}{l}$ (1)
Substituting $k = K$, \[A = {A_1}\], $l = L$, $\Delta T = {T_2} - {T_1}$, $q = Q$ and $T = t$, we get
$\dfrac{Q}{t} = K\dfrac{{{A_1}\left( {{T_2} - {T_1}} \right)}}{L}$....................(2)
Now, according to the question, the rod is melted and from that a new rod of half the radius is formed. We know that the area of cross section is related to the radius as
${A_1} = \pi {r^2}$................(3)
Putting $r' = \dfrac{r}{2}$, we get
${A_2} = \pi {\left( {\dfrac{r}{2}} \right)^2}$
${A_2} = \dfrac{{\pi {r^2}}}{4}$
Putting (3) in the above equation, we get
${A_2} = \dfrac{{{A_1}}}{4}$...................(4)
Since the material of the rod is still the same, there is no change in the thermal conductivity. Also, there is no change in the length and the temperature of the reservoirs. Therefore, if $Q'$ is the heat conducted by the new rod in time $t$, then it is given by
$\dfrac{{Q'}}{t} = K\dfrac{{{A_2}\left( {{T_2} - {T_1}} \right)}}{L}$ ……………...(5)
Dividing (5) by (2) we get
$\dfrac{{\dfrac{{Q'}}{t}}}{{\dfrac{Q}{t}}} = \dfrac{{K\dfrac{{{A_2}\left( {{T_2} - {T_1}} \right)}}{L}}}{{K\dfrac{{{A_1}\left( {{T_2} - {T_1}} \right)}}{L}}}$
\[ \Rightarrow \dfrac{{Q'}}{Q} = \dfrac{{{A_2}}}{{{A_1}}}\]
Putting (4) above, we get
\[\dfrac{{Q'}}{Q} = \dfrac{{{A_1}}}{{4{A_1}}}\]
\[ \Rightarrow Q' = \dfrac{Q}{4}\]

Hence, the correct answer is option A.

Note: If we do not remember the formula for the heat conducted per unit time, then we can use the analogy between the electric current and the heat to derive the same. As we know that the resistance is given by $R = \rho \dfrac{l}{A}$ and the electric current is given by $I = \dfrac{V}{R}$. Combining these two, we get the current as $I = \dfrac{{AV}}{{\rho l}}$. The electric current is equivalent to the heat per unit time, the potential difference is equivalent to the temperature difference, and the reciprocal of resistivity is equivalent to the thermal conductivity.