Question

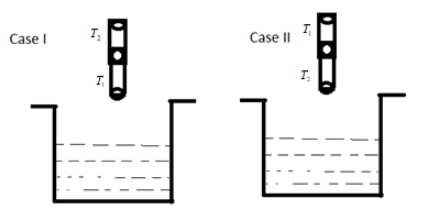
A cylindrical capillary tube \[ 0.2mm\] radius is made by joining two capillaries \[{T_1}\] and \[{T_2}\] of different materials having water contact angles of \[0^\circ \]and \[60^\circ \] respectively. The capillary tube is dipped vertically in water in two different configurations, case I and case II as shown in the figure. Which of the following option(s) are correct?

This question has multiple correct options:
$(A)$ For case I, if the joint is kept at \[8cm\] above the water surface, the height of the water column in the tube will be \[7.5cm\]. (Neglect the weight of the water in the meniscus)
\[(B)\] For the case I, the capillary joint is \[5cm\] above the water surface, the height of the water column raised in the tube will be more than \[8.75cm\]. (Neglect the weight of the water in the meniscus)
\[(C)\] The correction in the height of the water column raised in the tube, due to the weight of water contained in the meniscus, will be different for both cases.
\[(D)\] For case II, the capacity joint is \[5cm\] above the water surface, the height of the water column raised in the tube will be \[3.75cm\]. (Neglect the weight of the water in the meniscus)

Answer 1

Hint:Capillary tube is a cylindrical tube that forms a meniscus when it is dipped inside the water. The meniscus is the spherical curve that forms on the surface of the water. That meniscus has a radius. That radius of the meniscus depends upon the radius of the capillary tube. If the radius of the capillary tube is narrower, the curvature of the meniscus will be greater. If the radius of the capillary tube is wider, the curvature of the meniscus will be smaller.

Formula used:
\[h = \dfrac{{2T\cos \theta }}{{\rho rg}}\]
Where, \[h\]= Height of the water, \[T\]=Surface Tension of water\[(T = 0.075N/m)\], \[\theta \]= Contact angle created, \[\rho \]= Density of the water\[(1000Kg{m^{ - 3}})\], \[r\] = Radius of the capillary tube and \[g\]= Acceleration due to gravity\[(10m{s^{ - 2}})\].

Complete step by step answer:
Here the capillary tubes are joining together. This capillary tube is dipped vertically into the water. This is done in two ways. In the first case, the \[{T_1}\] side of the capillary tube is dipped. And in case II, \[{T_2}\] the side of the capillary tube is dipped.When the capillary tube is dipped, the level of water is raised inside the capillary tube. This rising of water causes meniscus. The height of the water rising can be found by the formula,
\[h = \dfrac{{2T\cos \theta }}{{\rho rg}}\]
When the \[{T_1}\] is dipped, the angle \[0^\circ \] is created. In this case, the height of the water can be found by the following method.
\[h = \dfrac{{2T\cos \theta }}{{\rho rg}}\]
\[ \Rightarrow h = \dfrac{{2 \times 0.075 \times \cos 0^\circ }}{{1000 \times 0.2 \times {{10}^{ - 3}} \times 10}}\]
\[h = 7.5cm\] ------------- (1)
In case II, the \[{T_2}\] side of the capillary tube is dipped, it makes \[60^\circ \] as a contact angle in the water. The height of the water is raised inside the capillary tube can be found by,
\[h = \dfrac{{2T\cos \theta }}{{\rho rg}}\]
\[ \Rightarrow h = \dfrac{{2 \times 0.075 \times \cos 60^\circ }}{{1000 \times 0.2 \times {{10}^{ - 3}} \times 10}}\]
\[\therefore h = 3.75cm\] -------------- (2)

Now let’s analyse the options. Option A can be correct. Because the height of the water inside the capillary tube is \[7.5cm\] in case I.Option B can be omitted as it recommends the height of the water inside the capillary tube is \[8.75cm\]. Therefore option B is incorrect.

Option C also can be omitted as it says that the height of the water rising depends upon the weight of the water in the meniscus. Because from the formula itself we can say that there is no place for the weight of the water in finding height. The option D is acceptable because, from equation (2), the height of the water raised in case II is \[3.75cm\]. Hence it is correct.

Therefore the options $(A)$ and \[(D)\] are correct.

Note:When the capillary tube is dipped in the water, it forms a meniscus. This meniscus is formed due to the contact angle between the water and the walls of the capillary tube. The water raised in the capillary tube depends upon the surface tension of the water, the contact angle created the density of the water, the radius of the cylindrical capillary tube, and the acceleration due to gravity.