Question

A cuboidal water tank contains $ 216 $ litres of water. Its depth is $ \dfrac{1}{3} $ of its length and breadth is $ \dfrac{1}{2}of\dfrac{1}{3} $ of the difference between length and depth. The length of the tank is
(A) $ 720dm $
(B) $ 18dm $
(C) $ 6dm $
(D) $ 2h\,dm $

Answer 1

Hint: In statement we see that the depth of the water tank is $ \dfrac{1}{3} $ of the length. Therefore, we first let the length of water tank as ‘x’ then using it we can find breadth, and depth in terms of ‘x’ of water tank. And then using length, breadth, and depth in volume formula to form an equation, which on simplification gives value of ‘x’ and hence length of the tank.
Volume of cuboidal water tank is $ Length\,(L) \times Breadth\,(B) \times Depth\,(D) $

Complete step-by-step answer:

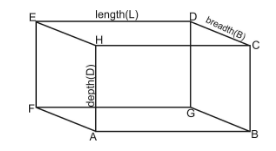
Volume of the cuboidal water tank is $ 216 $ litres.
Or writing volume in dm
We know that $ 1litres = 1\,d{m^3} $
 $ \therefore 216Litres = 216\,d{m^3} $
Also, from the statement we see that the depth of the cuboidal water tank depends on the length of the water tank.
 As, it is given that depth is $ \dfrac{1}{3} $ of length of water tank.
So, we let length of water tank = x
 Then, depth of water tank will be = $ \dfrac{1}{3}x $
Also, it is given that the breadth of the water tank is $ \dfrac{1}{2}of\dfrac{1}{3} $ of the difference between length and depth.
 $ \therefore $ Breadth of water tank = $ \dfrac{1}{2}of\dfrac{1}{3}\left( {lenght - depth} \right) $
 $ \Rightarrow breadth\,\,of\,\,water\,\,\tan k = \dfrac{1}{6}\left( {length - depth} \right) $
Substituting values of length and depth in the above equation to find breadth of water tank.
Breadth of water tank = $ \dfrac{1}{6}\left( {x - \dfrac{1}{3}x} \right) $
 $ \Rightarrow $ Breadth of water tank = $ \dfrac{1}{6}\left( {\dfrac{{3x - x}}{3}} \right) $
= $ \dfrac{1}{6}\left( {\dfrac{{2x}}{3}} \right) $
 $ = \dfrac{1}{9}x $
Therefore, from above we see that length, breadth and depth of water tank are $ x,\,\,\dfrac{1}{9}x\,\,and\,\,\dfrac{1}{3}x $ respectively.
Also, we know that volume of cuboidal water tank is given as $ Length(L) \times Breadth(B) \times Depth(D) $
 $ \Rightarrow Volume = L \times B \times D $
Substituting values in above formula we have
 $ 216 = \left( x \right) \times \left( {\dfrac{1}{9}x} \right) \times \left( {\dfrac{1}{3}x} \right) $
On simplifying right hand side of above equation
 $ 216 = \dfrac{{{x^3}}}{{27}} $
 $
   \Rightarrow {x^3} = 216 \times 27 \\
   \Rightarrow {x^3} = {6^3} \times {3^3} \\
   \Rightarrow {x^3} = {\left( {18} \right)^3} \\
  $
 $ \Rightarrow x = 18 $
Substituting value of x = $ 18 $ to find respective length, breadth and depth of water tank.
Length of water tank = x = $ 18 $
Breadth of water tank = $ \dfrac{1}{9}x = \dfrac{1}{9}\left( {18} \right) = 2 $
Depth of water tank = $ \dfrac{1}{3}x = \dfrac{1}{3}(18) = 6 $
Therefore from above we see that length = $ 18\,dm $ , breadth = $ 2\,dm $ and depth = $ 6\,dm $ are respectively.
Hence, from the given option we see that the correct option is (B) as the length of the water tank is $ 18\,dm $ .
So, the correct answer is “Option B”.

Note: While doing mensuration problems we first convert all given terms in the same unit. If there are different terms with different units and then do calculations very carefully. As, while doing calculations in mensuration problems students may make silly mistakes in calculations which lead to wrong answers to the problem.