
A cottage industry manufactures pedestal lamps and wooden shades, each requiring the use of a grinding/cutting machine and a sprayer. It takes 2 hours on the grinding/cutting machines and 3 hours on the sprayer to manufacture a pedestal lamp. It takes 1 hour on the grinding/cutting machine and 2 hours on the sprayer to manufacture a shade. On any day, the sprayer is available for at least for at the most 20 hours and the grinding/cutting machine for at the most 12 hours. The profit from the sale of a lamp is Rs.5 and that from a shade is Rs. 3. Assuming that the manufacturer can sell all the lamps and shades that the produces, how should he schedule his daily production in order to maximize his profit?
Answer
582k+ views
Hint: First of all, let the number of pedestal lamps that are to be made is $x$ and the number of wooden shades that are to be made be $y$. Then, use the given conditions to form the corresponding linear programming problem. Solve the problem by using the graph method. Find the value of the objective function at the corner points. Then, the value at which the profit is maximum is the optimal value.
Complete step by step Answer:
We will begin by letting the number of pedestal lamps that are to be made is $x$ and the number of wooden shades that are to be made be $y$.
We are given that the pedestal lamps require 2 hours of grinding/cutting and wooden shades require 1 hour of grinding/cutting and there are maximum 12 hours for cutting/grinding.
Then, we can say that $2x + y \leqslant 12$ (1)
Similarly, we are also given that the pedestal lamps require 3 hours of sprayer whereas the wooden shades require 2 hours for the sprayer. Also, the maximum number of hours available for sprayer is 20 hours.
Hence, $3x + 2y \leqslant 20$ (2)
Also, the number of pedestal lamps and wooden shades cannot be negative.
Therefore, $x \geqslant 0,y \geqslant 0$
We have to maximize profit.
We are given that the profit on a pedestal lamp is Rs. 5 and the profit on wooden shades is Rs.3.
Hence, we have to maximize $Z = 5x + 3y$
We will solve the linear programming problem:
Maximize $Z = 5x + 3y$
Subject to $2x + y \leqslant 12$
And $3x + 2y \leqslant 20$
$x \geqslant 0,y \geqslant 0$
We will first plot the linear inequalities and plot the boundary points.
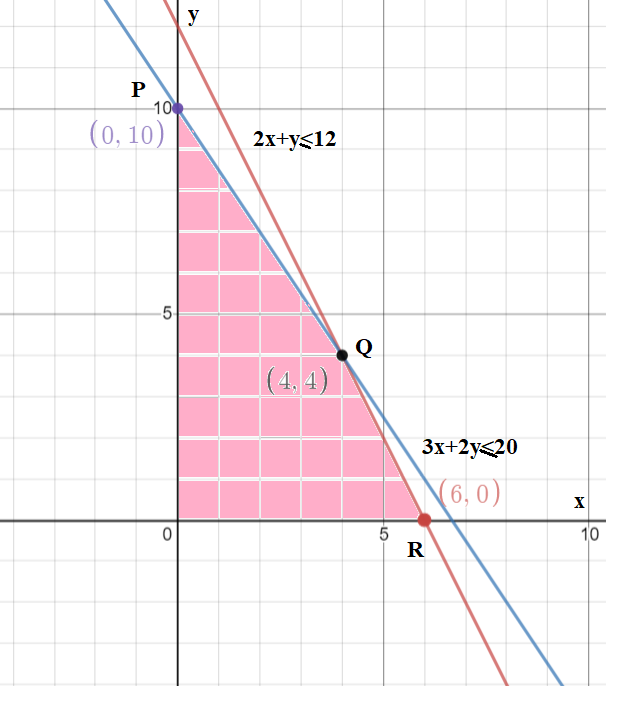
The value of the function $Z = 5x + 3y$ at boundary points is:
The maximum value is at the point Q$\left( {4,4} \right)$
Hence, industry should produce 4 units of pedestal lamp and 4 units of wooden shades in order to maximise profit.
Note: We use linear programming method when we have limit resources and have to use most of it. In this type of questions, many students are unable to translate the description in terms of inequalities correctly. Here, we were the maximum of the resources and hence we used the less than equal to sign. Also, the shading of the area should be done correctly.
Complete step by step Answer:
We will begin by letting the number of pedestal lamps that are to be made is $x$ and the number of wooden shades that are to be made be $y$.
We are given that the pedestal lamps require 2 hours of grinding/cutting and wooden shades require 1 hour of grinding/cutting and there are maximum 12 hours for cutting/grinding.
Then, we can say that $2x + y \leqslant 12$ (1)
Similarly, we are also given that the pedestal lamps require 3 hours of sprayer whereas the wooden shades require 2 hours for the sprayer. Also, the maximum number of hours available for sprayer is 20 hours.
Hence, $3x + 2y \leqslant 20$ (2)
Also, the number of pedestal lamps and wooden shades cannot be negative.
Therefore, $x \geqslant 0,y \geqslant 0$
We have to maximize profit.
We are given that the profit on a pedestal lamp is Rs. 5 and the profit on wooden shades is Rs.3.
Hence, we have to maximize $Z = 5x + 3y$
We will solve the linear programming problem:
Maximize $Z = 5x + 3y$
Subject to $2x + y \leqslant 12$
And $3x + 2y \leqslant 20$
$x \geqslant 0,y \geqslant 0$
We will first plot the linear inequalities and plot the boundary points.

The value of the function $Z = 5x + 3y$ at boundary points is:
| Point | $Z = 5x + 3y$ |
| P$\left( {0,10} \right)$ | $5\left( 0 \right) + 3\left( {10} \right) = 30$ |
| Q$\left( {4,4} \right)$ | $5\left( 4 \right) + 3\left( 4 \right) = 32$ |
| R\[\left( {6,0} \right)\] | $5\left( 6 \right) + 3\left( 0 \right) = 30$ |
The maximum value is at the point Q$\left( {4,4} \right)$
Hence, industry should produce 4 units of pedestal lamp and 4 units of wooden shades in order to maximise profit.
Note: We use linear programming method when we have limit resources and have to use most of it. In this type of questions, many students are unable to translate the description in terms of inequalities correctly. Here, we were the maximum of the resources and hence we used the less than equal to sign. Also, the shading of the area should be done correctly.
Recently Updated Pages
The number of solutions in x in 02pi for which sqrt class 12 maths CBSE

Write any two methods of preparation of phenol Give class 12 chemistry CBSE

Differentiate between action potential and resting class 12 biology CBSE

Two plane mirrors arranged at right angles to each class 12 physics CBSE

Which of the following molecules is are chiral A I class 12 chemistry CBSE

Name different types of neurons and give one function class 12 biology CBSE

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

What is 1s 2s 2p 3s 3p class 11 chemistry CBSE

Discuss the various forms of bacteria class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE

An example of chemosynthetic bacteria is A E coli B class 11 biology CBSE




