Question

A container open from the top, made up of a metal sheet is in the form of a frustum of a cone of height 8cm with radii of its lower and upper end as 4cm and 10cm respectively. Find the cost of milk which can completely fill the container at the rate of Rs.50 per litre and the cost of metal sheet used, if it costs Rs.50 per 100cm2. (Use \[\pi =3.14\])

Answer 1

Hint: We need to calculate the total volume and the total surface area of the frustum of a cone to find the cost of milk that can completely fill the container and the cost of metal sheet used.

We know the formulae for volume and surface area of frustum of a cone
\[\text{volume }\left( v \right)=\dfrac{1}{3}\pi h\left( {{r}^{2}}+{{R}^{2}}+rR \right)..........\left( 1 \right)\]
\[\text{Total surface area with open from top = curved surface area + base area}\]
\[\begin{align}
  & \text{TSA=}\pi \times l\left( R+r \right)+\pi {{R}^{2}} \\
 & \text{TSA=}\pi \left( R+r \right)\sqrt{{{\left( R-r \right)}^{2}}+{{h}^{2}}}+\pi {{R}^{2}}.............\left( 2 \right) \\
\end{align}\]
Where r = radius of lower end
             R = radius of upper end
             h = height of frustum
             l = slant height of frustum
 

From the question given that
Height of the frustum IH (h) = 8cm
Radius of lower end AH (R) =4cm
Radius of upper end EI (r) = 10cm
Now to find the cost of milk that completely fills the frustum of cone we need to find the volume of frustum of cone
From the above formula of volume of frustum of cone (1) by substituting the values h=8cm, r=4cm, R=10cm we get,
\[\begin{align}
  & v=\dfrac{1}{3}\pi h\left( {{r}^{2}}+{{R}^{2}}+rR \right) \\
 & \Rightarrow v\text{=}\dfrac{1}{3}\times \pi \times 8\left[ {{\left( 4 \right)}^{2}}+{{\left( 10 \right)}^{2}}+4\times 10 \right] \\
 & \Rightarrow v=\dfrac{1}{3}\times \pi \times 8\left[ 16+100+40 \right] \\
 & \Rightarrow v=\dfrac{1}{3}\times \pi \times 8\left[ 156 \right] \\
 & \Rightarrow v=\dfrac{1}{3}\times 3.14\times 8\times 156\text{ }\left( \because \pi =3.14 \right) \\
 & \Rightarrow v=\dfrac{3918.32}{3} \\
 & \therefore v=1306.24\text{ c}{{\text{m}}^{3}} \\
\end{align}\]
As we know that from the standard conversions
\[1\text{ litre = 1000 c}{{\text{m}}^{3}}\]
\[\therefore 1\text{ c}{{\text{m}}^{3}}\text{= 0}\text{.001 litre}\]
Now by applying the above conversion to the volume of frustum of cone obtained we get
\[\begin{align}
  & \Rightarrow v=\dfrac{1306.24}{1000}\text{ litre} \\
 & \Rightarrow v=1.30624\text{ litre} \\
 & \therefore v\approx 1.306\text{ litre} \\
\end{align}\]
Given that the rate of milk per litre is Rs.50
\[\begin{align}
  & \text{cost of milk per litre = Rs}\text{.50} \\
 & \text{cost of milk per 1}\text{.306 litre = Rs}\text{.}\left( 1.306\times 50 \right) \\
 & \text{cost of milk per 1}\text{.306 litre = Rs}\text{.65}\text{.3} \\
 & \therefore \text{cost of milk which can completely fill the container = Rs}\text{.65}\text{.3} \\
\end{align}\]
Now we need to find the cost of metal sheet used for that we need to calcite the total surface area because here the metal sheet is folded in the form of frustum of a cone which covers the surface area
As we know the formula of total surface area of a frustum open from top (2) we get,
TSA = Curved surface area + base area
\[\text{TSA=}\pi \left( R+r \right)\sqrt{{{\left( R-r \right)}^{2}}+{{h}^{2}}}+\pi {{R}^{2}}\]
By substituting the values of R= 4cm, r= 10cm, h=8cm in formula (2)
\[\begin{align}
  & \Rightarrow \text{TSA=}\pi \left( 10+4 \right)\sqrt{{{\left( 10-4 \right)}^{2}}+{{8}^{2}}}+\pi {{\left( 4 \right)}^{2}} \\
 & \Rightarrow \text{TSA=}\pi \left( 14 \right)\sqrt{{{6}^{2}}+{{8}^{2}}}+\pi \left( 16 \right) \\
 & \Rightarrow \text{TSA=}\pi \left( 14 \right)\sqrt{36+64}+\pi \left( 16 \right) \\
 & \Rightarrow \text{TSA=}3.14\left( 14 \right)\sqrt{100}+3.14\left( 16 \right) \\
 & \Rightarrow \text{TSA=}3.14\left( 14 \right)\left( 10 \right)+50.24 \\
 & \Rightarrow \text{TSA=}3.14\left( 140 \right)+50.24 \\
 & \Rightarrow \text{TSA=}439.6+50.24 \\
 & \therefore \text{TSA=}489.84\text{ c}{{\text{m}}^{2}} \\
\end{align}\]
In the question given that metal costs Rs.50 per 100 cm2
Let us assume that the cost of metal sheet per 489.84 cm2 as x
Now from algebra we can calculate the value of x by using cross multiplication method
\[\begin{align}
  & \Rightarrow x\times 100=50\times 489.84 \\
 & \Rightarrow x=\dfrac{50\times 489.84}{100} \\
 & \Rightarrow x=\dfrac{24492}{100} \\
 & \therefore x=244.92 \\
 & \therefore \text{cost of metal sheet used = Rs}\text{.244}\text{.92} \\
\end{align}\]

Note:
While calculating the surface area we wrote slant height in terms of lower end radius, upper end radius and height of frustum by applying the Pythagoras Theorem.

 

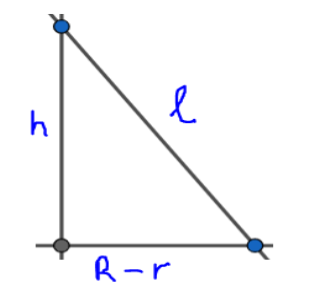
\[\begin{align}
  & {{l}^{2}}={{h}^{2}}+{{\left( R-r \right)}^{2}} \\
 & \therefore l=\sqrt{{{h}^{2}}+{{\left( R-r \right)}^{2}}} \\
\end{align}\]
In calculating the total surface area, we only considered curved surface area and base area but not the top area because given that container is open from top. so, here we should not consider the top area while calculating the total surface area if considering, it gives the wrong result.
For calculating the cost of metal sheet used we can evaluate it in other way directly instead of using the, cross multiplication method by the following method
\[\begin{align}
  & \text{cost of metal sheet per 100c}{{\text{m}}^{2}}=Rs.50 \\
 & \text{cost of metal sheet per 489}\text{.84c}{{\text{m}}^{2}}=Rs.\left( \dfrac{50\times 489.84}{100} \right) \\
 & \therefore \text{cost of metal sheet per 489}\text{.84c}{{\text{m}}^{2}}=Rs.244.92 \\
\end{align}\]
This also gives the same result the only difference here is we are not assuming any x and directly calculating the cost.