Question

A constant force F is applied in a horizontal direction as shown. The contact force between M and m is N and between m and M’ is N’ then:

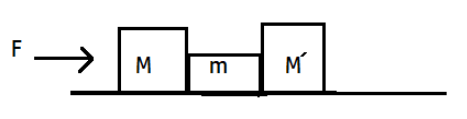
(A) N=N’
(B) N>N’
(C)N’>N
(D) cannot be determined from the given data

Answer 1

Hint: Here we have three bodies of given masses and placed close to each other in contact. The floor is smooth and there is no scope of any frictional force present. A constant force F acts on the first body and we need to find the force between the masses. Newton’s third law of motion can be used here.

Complete step by step answer:

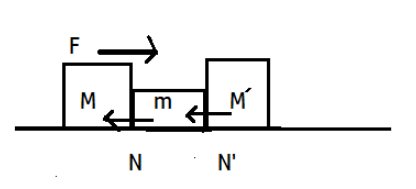
Since F acts on the M and this is constant, if we see the whole system then the total mass of the system is (M+m+M’)
Applying Newton’s second law we get, F=(M+m+M’)a
\[a=\dfrac{F}{M+m+M'}\]
Between M and m contact force is N, applying Newton’s third law
\[N=\dfrac{(m+M')F}{M+m+M'}\]-----(1)
Between m and M’ contact force is N’, applying Newton’s third law \[N'=\dfrac{M'F}{M+m+M'}\]----(2)
Comparing the above two it is visible that numerator of (1) is greater than the numerator of (2) while the denominators are same, so, N>N’

Hence, the correct option is (B).

Note:Newton’s second law states that force applied on a body is equal to the product of the mass of the body and acceleration produced in the body. If the external force is zero, then the acceleration of the body is zero. Newton’s third law states that forces always occur in pairs.