Question

A conical tent is 10 m high and the radius of its base is 24 m. Find slant height of the tent and cost of the canvas required to make the tent, if the cost of 1 square meter canvas is Rs. 70.

Answer 1

Hint: We know the formula for slant height of the conical tent is, \[{l^2} = {h^2} + {r^2}\] where the height of the conical tent is \[h\] and \[r\] is the radius of the conical tent. To find the cost we find the curved surface area of the tent and we know the cost of 1 square meter canvas is rupees 70. The value of \[\pi \] is \[\pi = \dfrac{{22}}{7}\] .

Complete step-by-step answer:

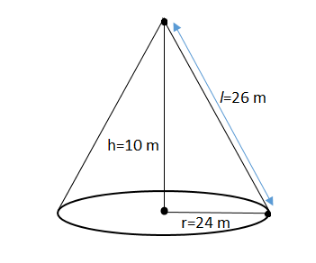
We have the formula \[{l^2} = {h^2} + {r^2}\] ,
Given, \[h = 10 \;m\] , \[r = 24 \;m\] and we need to find \[l\] .
Substituting we have,
 \[ \Rightarrow {l^2} = {(10)^2} + {(24)^2}\]
 \[ \Rightarrow {l^2} = 100 + 576\]
 \[ \Rightarrow {l^2} = 676\]
 \[ \Rightarrow l = \sqrt {676} \]
We know that 26 square is 676
 \[ \Rightarrow l = \sqrt {{{26}^2}} \]
Cancelling square and square root we get,
 \[ \Rightarrow l = 26\]
Hence, the slant height of the tent is 26 m.
To find the cost:
Here the tent does not cover the base, so we find the curved surface area of the tent.
We know that the curved surface area of tent \[ = \pi rl{\text{ }}{{\text{m}}^2}\]
We have, \[l = 26 \;m\] and \[r = 24 \;m\] , substituting we have,
 \[ \Rightarrow \dfrac{{22}}{7} \times 24 \times 26\]
 \[ \Rightarrow \dfrac{{13728}}{7}{m^2}\]
We have a cost of 1 \[{m^2}\] canvas = Rs. 70.
The Cost of \[\dfrac{{13728}}{7}{m^2}\] \[ = Rs.\dfrac{{13728}}{7} \times 70\]
 \[ \Rightarrow Rs.137280\]
So, the correct answer is “Rs.137280”.

Note: In the case of conical shape objects slant height and height are different. Also the surface area of the cone and the curved surface area cone are different. The total surface area of the cone is \[ = \pi r(r + l)\] . Area always needs to be in square meters. Always observe the units of radius and height, all should be in the same. If not convert it.