Question

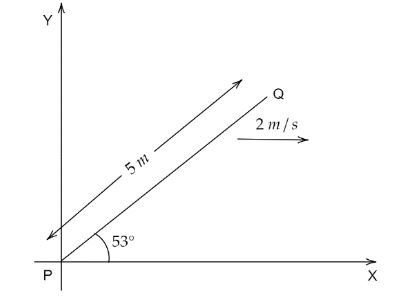
A conducting rod PQ of length $5{\text{ }}m$ oriented as shown in figure is moving with velocity $\left( {2{\text{ }}\dfrac{m}{s}} \right)\widehat i$ without rotation in a uniform magnetic field $\left( {3\widehat j + 4\widehat k} \right){\text{ }}Tesla$. The emf induced in the rod is

A. $32{\text{ }}Volts$
B. ${\text{40 }}Volts$
C. ${\text{50 }}Volts$
D. none

Answer 1

Hint: In the given question, we are given with the magnitude of the length of the rod. We have to convert it to vector form in order to solve the equation. Then by using the formula of induced emf in vector form we will find the answer.

Complete step by step answer:
It is given in the question that the length $l$ of the conducting rod PQ is $5{\text{ }}m$. The velocity $\overrightarrow v $ is given in the X-direction, $\left( {2{\text{ }}\dfrac{m}{s}} \right)\widehat i$. The uniform magnetic field $\overrightarrow B $ associated with the rod PQ is $\left( {3\widehat j + 4\widehat k} \right){\text{ }}Tesla$.

Now, the vector form of the length of the rod is,
$\overrightarrow l = l\cos {53^ \circ }\overrightarrow i + l\sin {53^ \circ }\overrightarrow j $
Substituting the value of length $l = 5{\text{ }}m$
$\overrightarrow l = 5\cos {53^ \circ }\overrightarrow i + 5\sin {53^ \circ }\overrightarrow j $
$\therefore \overrightarrow l = 3\overrightarrow i + 4\overrightarrow j $
The formula for the induced emf in vector form is $\left| {\left( {\overrightarrow v \times \overrightarrow B } \right).\overrightarrow l } \right|$

Firstly, let us solve, $\left( {\overrightarrow v \times \overrightarrow B } \right)$,
Substituting the value of uniform magnetic field $\overrightarrow B $ and velocity $\overrightarrow v $ and getting the cross-product of them as,
$\left( {\overrightarrow v \times \overrightarrow B } \right) = \left[ {2\widehat i \times \left( {3\widehat j + 4\widehat k} \right)} \right] = 6\overrightarrow k - 8\overrightarrow j $
Hence, we got the value of $\left( {\overrightarrow v \times \overrightarrow B } \right) = 6\overrightarrow k - 8\overrightarrow j $

Now, by the dot product of $\left( {\overrightarrow v \times \overrightarrow B } \right)$ and $\overrightarrow l $ will give the emf of the rod,
Thus, $\left( {\overrightarrow v \times \overrightarrow B } \right).\overrightarrow l = \left( {6\overrightarrow k - 8\overrightarrow j } \right).3\overrightarrow i + 4\overrightarrow j = - 32$
Therefore, the emf of the rod is, $\left| {\left( {\overrightarrow v \times \overrightarrow B } \right).\overrightarrow l } \right| = \left| { - 32} \right| = 32$
So, the emf of the rod is $32{\text{ }}Volts$.

Therefore, the correct option is A.

Note:It must be noted that emf is defined as the electric potential developed due to changing magnetic fields. The vector cross-product is involved with the direction vectors which must be calculated carefully. In the case of a dot product of vectors, the direction of the vector's multiplication results in value $1$ and unlike direction corresponds to $0$.