Question

A closed conical is filled with water fully and is placed with its vertex down. The water is let out at a constant speed after \[21\] minutes, it was found that the height of the water column is half of the original height. How much more time in minutes does it empty the vessel?
A) $21$
B) $14$
C) $7$
D) $3$

Answer 1

Hint:We will use the fact that the rate of output is constant at any point. Also, we will use the given data to establish the connection between the rate of depletion of water level and time taken to fill the vessel. We will use the initial condition and then solve the obtained equation.

Complete step-by-step answer:
Note that the conical vessel is put in a vertex down position.
Consider the following schematic figure to understand the position of the vessel.

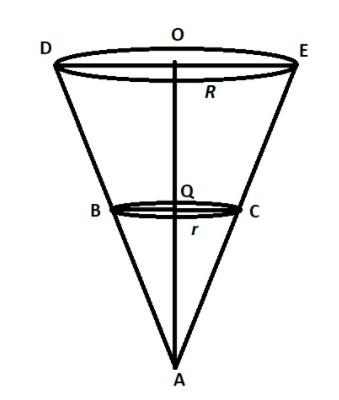
The radius at the top is $R$ .
Therefore, the volume of the water after the vessel is full is the same as the volume of the vessel.
${V_1} = \dfrac{1}{3}\pi {R^2}h$ … (1)
Now it is given that the volume of the water inside the cone after $21$ minutes is half that means it is the same as the volume of the smaller cone $ABC$ .
Suppose that the smaller radius is $r$ .
From the given data the height of that cone is $\dfrac{h}{2}$.
Therefore, volume of the smaller cone is:
${V_2} = \dfrac{1}{6}\pi {r^2}h$
Now in the figure we observe that the triangle $\Delta AOD$ and $\Delta AQB$ are similar triangles as they have two pairs of congruent angles i.e. using AA test of similarity.
Therefore, using the corresponding ratio of the sides,
$\dfrac{{AO}}{{AQ}} = \dfrac{{OD}}{{QB}}$
Now substitute the respective values of the sides and obtain the following:
$\dfrac{h}{{\dfrac{h}{2}}} = \dfrac{R}{r}$
On simplifying the terms, we write $R = 2r$ .
Substituting in equation (1),
${V_1} = \dfrac{4}{3}\pi {r^2}h$
Therefore, volume went out after $21$ minutes is the difference between two quantities of volume.
$\dfrac{4}{3}\pi {r^2}h - \dfrac{1}{6}\pi {r^2}h = \dfrac{7}{6}\pi {r^2}h$
Therefore, we conclude that $\dfrac{7}{6}\pi {r^2}h$ cubic units water flows in $21$ min.
Thus, time taken by the vessel to throw out $1$ cubic units of water is $\dfrac{{21 \times 6}}{{7\pi {r^2}h}}$.
We have left with $\dfrac{1}{6}\pi {r^2}h$ cubic units of water.
The time taken for that to flow out is:
$\dfrac{{21 \times 6}}{{7\pi {r^2}h}} \times \dfrac{1}{6}\pi {r^2}h = 3$
Thus, time taken to empty the remaining vessel is $3$ min.

So, the correct answer is “Option D”.

Note:The given example contains a lot of complications so consider each condition one by one before reaching the final conclusion. Use the time given in each case and relate it with the left-out volume properly. Don’t let the words like rate and speed confuse you the problem is very basic and doesn’t involve any derivative etc.